Question

【题目】设函数f（x）＝asinωx+bcosωx（ω＞0）的定义域为R，最小正周期为π，且对任意实数x，恒有成立．

（1）求实数a和b的值；

（2）作出函数f（x）在区间（0，π）上的大致图象；

（3）若两相异实数x1、x2∈（0，π），且满足f（x1）＝f（x2），求f（x1+x2）的值．

Answer 1

【答案】（1）a＝2，b＝2．（2）见解析 （3）f（x1+x2）＝2．

【解析】

（1）将f（x）＝asinωx+bcosωx化为f（x）sin（ωx+φ），由题意可得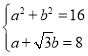，从而可求得a和b的值；

（2）由f（x）＝4sin（2x）利用五点作图法即可作出其大致图象；

（3）当0＜x1＜x2时，x1+x2，当x1＜x2＜π时，x1+x2，从而可求得f（x1+x2）的值．

解（1）∵f（x）＝asinωx+bcosωxsin（ωx+φ）（ω＞0），

又f（x）≤f（）＝4恒成立，

∴4，即a2+b2＝16．…①

∵f（x）的最小正周期为π，

∴ω2，

即f（x）＝asin2x+bcos2x（ω＞0）．

又f（x）max＝f（）＝4，

∴asinbcos4，

即ab＝8．…②

由①、②解得a＝2，b＝2．

（2）由（1）知f（x）＝2sin2x+2cos2x＝4sin（2x）．

∵0＜x＜π，

∴2x，列表如下：

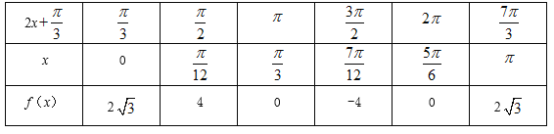
∴函数f（x）的图象如图所示：

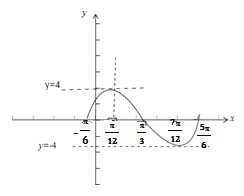
（3）∵f（x1）＝f（x2），由f（x）＝4sin（2x）知，f（0）＝f（）＝2，

如图：

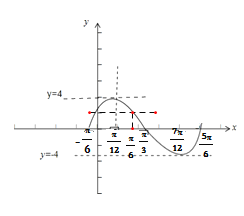
∴当0＜x1＜x2时，x1+x2＝2，

∴f（x1+x2）＝f（）＝42；

当x1＜x2＜π时，x1+x2＝2，

∴f（x1+x2）＝f（）＝4sin2

综上，f（x1+x2）＝2．