��Ŀ����
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ����Ϊ�˱������������ٿ�����Ⱦ��ij�������������쳧������Ͷ������ij�ֻ����͵Ŀ����������������������������۾���õ����������۵�ͳ�ƹ������£�����̶������ɱ�Ϊ2��Ԫ����ÿ�������ͺſ���������1��̨���ɱ�����1��Ԫ����������x��̨���������� ����Ԫ�����ٶ������ĸ��ͺſ������������������������������멁�����ɱ�����
����Ԫ�����ٶ������ĸ��ͺſ������������������������������멁�����ɱ�����
��1��Ϊʹ�ò�Ʒ�������������������xӦ������ʲô��Χ�ڣ�
��2���ò�Ʒ��������̨ʱ����ʹ���������
���𰸡���1��100̨��550̨֮�䣻��2�����300̨ʱ����ʹ�������
��������
��1�������⣬�ɱ�����Ϊ![]() ���Ӷ���������Ϊ
���Ӷ���������Ϊ![]() ��Ҫʹ�����������÷ֶκ����Ͷ��κ��������ʣ�������⣮
��Ҫʹ�����������÷ֶκ����Ͷ��κ��������ʣ�������⣮
��2�����÷ֶκ��������ÿ֧�ϵ����ֵ�����ɵõ����������ֵ���õ��𰸣�
��1��������ã��ɱ�����Ϊ![]() ��
��
�Ӷ���������Ϊ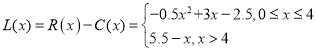 ��
��
Ҫʹ��������ֻҪL��x����0��
�ٵ�0��x��4ʱ����L��x����0�é�0.5x2+3x��2.5��0, ���1��x��4��
�ڵ�x��4ʱ����L��x����0��5.5��x��0, ���4��x��5.5
����1��x��5.5
����Ҫ�ó�������������xӦ������100̨��550̨֮��
��2����0��x��4ʱ��L��x��= -0.5(x��3)2+2��
�ʵ�x =3ʱ��L��x��max=2����Ԫ����
��x��4ʱ��L��x����1.5��2��
���ϣ������300̨ʱ����ʹ�������

 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�