题目内容
【题目】已知函数![]()
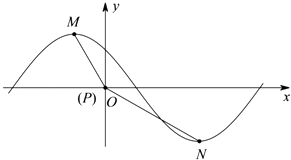
![]() 的一段图像如图所示.
的一段图像如图所示.

(1)求此函数的解析式;
(2)求此函数在![]() 上的单调递增区间.
上的单调递增区间.
【答案】(1)![]() ;(2)
;(2)![]() 和
和![]() .
.
【解析】
![]() 根据三角函数的图象求出
根据三角函数的图象求出![]() ,
,![]() ,即可确定出函数的解析式
,即可确定出函数的解析式
![]() 根据函数的表达式,即可求出函数的单调递增区间
根据函数的表达式,即可求出函数的单调递增区间
(1)由图可知,其振幅为A=2![]() ,
,
由于![]()
所以周期为T=16,
所以![]()
此时解析式为![]()
因为点(2,-2![]() )在函数
)在函数![]() 的图象上,
的图象上,
所以![]() 所以
所以![]()
又|φ|<π,所以![]()
故所求函数的解析式为![]()
(2)由![]() ,得16k+2≤x≤16k+10(k∈Z),
,得16k+2≤x≤16k+10(k∈Z),
所以函数![]() 的递增区间是[16k+2,16k+10](k∈Z).
的递增区间是[16k+2,16k+10](k∈Z).
当k=-1时,有递增区间[-14,-6],当k=0时,有递增区间[2,10],
与定义区间求交集得此函数在(-2π,2π)上的递增区间为(-2π,-6]和[2,2π).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目