题目内容
7.设函数f(x)=$\frac{{x}^{2}}{2}$-klnx,k>0.(1)求f(x)的单调区间和极值;
(2)证明:若f(x)存在零点,则f(x)在区间(1,$\sqrt{e}$]上仅有一个零点.
分析 (1)利用f'(x)≥0或f'(x)≤0求得函数的单调区间并能求出极值;
(2)利用函数的导数的极值求出最值,利用最值讨论存在零点的情况.
解答 解:(1)由f(x)=$\frac{{x}^{2}}{2}-klnx(k>0)\\;\\;得$
f'(x)=x-$\frac{k}{x}=\frac{{x}^{2}-k}{x}$
由f'(x)=0解得x=$\sqrt{k}$
f(x)与f'(x)在区间(0,+∞)上的情况如下:
| X | (0,$\sqrt{k}$) | $\sqrt{k}$ | ($\sqrt{k},+∞$) |
| f'(x) | - | 0 | + |
| f(x) | ↓ | $\frac{k(1-lnk)}{2}$ | ↑ |
f(x)在x=$\sqrt{k}$处的极小值为f($\sqrt{k}$)=$\frac{k(1-lnk)}{2}$,无极大值.
(2)证明:由(1)知,f(x)在区间(0,+∞)上的最小值为f($\sqrt{k}$)=$\frac{k(1-lnk)}{2}$.
因为f(x)存在零点,所以$\frac{k(1-lnk)}{2}≤0$,从而k≥e
当k=e时,f(x)在区间(1,$\sqrt{e}$)上单调递减,且f($\sqrt{e}$)=0
所以x=$\sqrt{e}$是f(x)在区间(1,$\sqrt{e}$)上唯一零点.
当k>e时,f(x)在区间(0,$\sqrt{e}$)上单调递减,且$f(1)=\frac{1}{2}>0,f(\sqrt{e})=\frac{e-k}{2}<0$,
所以f(x)在区间(1,$\sqrt{e}$)上仅有一个零点.
综上所述,若f(x)存在零点,则f(x)在区间(1,$\sqrt{e}$]上仅有一个零点.
点评 本题考查利用函数的导数求单调区间和导数的综合应用,在高考中属于常见题型.

练习册系列答案
相关题目
2.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )
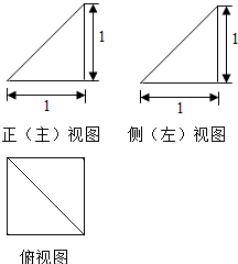

| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
19. 一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
 一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )
一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
17.设复数z满足$\frac{1+z}{1-z}$=i,则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |