题目内容
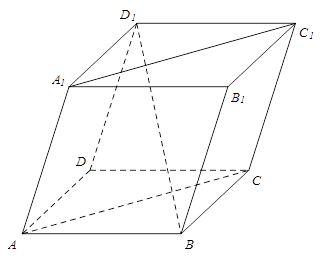
正△ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC—B。
(I)试判断直线AB与平面DEF的位置关系,并说明理由;
(II)求二面角E—DF—C的余弦值;
(III)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论。

(I)试判断直线AB与平面DEF的位置关系,并说明理由;
(II)求二面角E—DF—C的余弦值;
(III)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论。

解法一:(Ⅰ)如图:在 中,由
中,由 分别是
分别是 和
和 边的中点,得
边的中点,得 ,
,
又 平面
平面 ,
, 平面
平面 . ∴
. ∴ 平面
平面 . …………4分
. …………4分
(Ⅱ) ,∴
,∴ 是二面角
是二面角 的平面角,
的平面角, ,得
,得 平面
平面 .
.
取 的中点
的中点 ,连接
,连接 ,则
,则 , ∴
, ∴ 平面
平面 ,过
,过 作
作 于点
于点 ,连接
,连接 ,则根据三垂线定理知
,则根据三垂线定理知 ,∴
,∴ 就是二面角
就是二面角 的平面角.
的平面角.
在 中,
中, ,
, ,∴
,∴ ,
, .………8分
.………8分
(Ⅲ)在线段 上存在点
上存在点 ,使
,使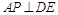 ,证明如下:
,证明如下:
在线段 上取点
上取点 ,使
,使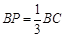 ,过
,过 作
作 与点
与点 ,连
,连 ,则
,则 平面
平面 ,
, ,于是有
,于是有 ,在
,在 中,
中, ,
, ;又∵
;又∵ 是正三角形,∴
是正三角形,∴ ,∴
,∴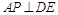 .………13分
.………13分
法二:(Ⅰ)同解法一.

(Ⅱ)以点 为坐标原点,直线
为坐标原点,直线 分别为
分别为 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则 ,
, ,
, ,
, ,
,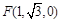 .
.
显然平面 的一个法向量为
的一个法向量为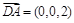 ,设平面
,设平面 的一个法向量为
的一个法向量为 ,则
,则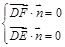 ,即
,即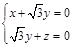 ,令
,令 得,
得, .
.  ,所以二面角
,所以二面角 的余弦值为
的余弦值为 .
.
(Ⅲ)设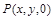 ,由
,由 ,得
,得 . 又
. 又 ,
, ,
, ,
, ;将
;将 代入上式,得
代入上式,得 ,
, ,所以在线段
,所以在线段 上存在点
上存在点 ,使
,使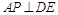 .
.
 中,由
中,由 分别是
分别是 和
和 边的中点,得
边的中点,得 ,
,又
 平面
平面 ,
, 平面
平面 . ∴
. ∴ 平面
平面 . …………4分
. …………4分 (Ⅱ)
 ,∴
,∴ 是二面角
是二面角 的平面角,
的平面角, ,得
,得 平面
平面 .
. 取
 的中点
的中点 ,连接
,连接 ,则
,则 , ∴
, ∴ 平面
平面 ,过
,过 作
作 于点
于点 ,连接
,连接 ,则根据三垂线定理知
,则根据三垂线定理知 ,∴
,∴ 就是二面角
就是二面角 的平面角.
的平面角.在
 中,
中, ,
, ,∴
,∴ ,
, .………8分
.………8分(Ⅲ)在线段
 上存在点
上存在点 ,使
,使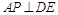 ,证明如下:
,证明如下:在线段
 上取点
上取点 ,使
,使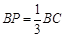 ,过
,过 作
作 与点
与点 ,连
,连 ,则
,则 平面
平面 ,
, ,于是有
,于是有 ,在
,在 中,
中, ,
, ;又∵
;又∵ 是正三角形,∴
是正三角形,∴ ,∴
,∴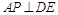 .………13分
.………13分法二:(Ⅰ)同解法一.

(Ⅱ)以点
 为坐标原点,直线
为坐标原点,直线 分别为
分别为 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则 ,
, ,
, ,
, ,
,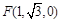 .
.显然平面
 的一个法向量为
的一个法向量为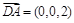 ,设平面
,设平面 的一个法向量为
的一个法向量为 ,则
,则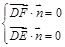 ,即
,即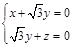 ,令
,令 得,
得, .
.  ,所以二面角
,所以二面角 的余弦值为
的余弦值为 .
.(Ⅲ)设
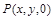 ,由
,由 ,得
,得 . 又
. 又 ,
, ,
, ,
, ;将
;将 代入上式,得
代入上式,得 ,
, ,所以在线段
,所以在线段 上存在点
上存在点 ,使
,使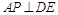 .
.略

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 的条件是( )
的条件是( )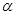 内有无数条直线平行于平面
内有无数条直线平行于平面
 .
.
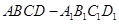 中,
中,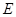 为
为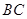 的中点,
的中点,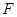 为
为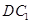 的中点.
的中点.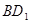 //平面
//平面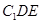 ;(2)求三棱锥
;(2)求三棱锥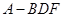 的体积;
的体积;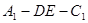 的余弦值。
的余弦值。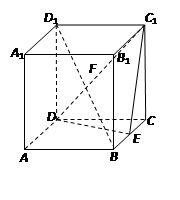
 沿对角线
沿对角线 折起,使平面
折起,使平面 平面
平面 ,
, 是
是 的中点,那么异面直线
的中点,那么异面直线 、
、 所成的角的正切值为 。
所成的角的正切值为 。
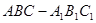 的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,
的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,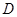 为
为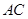 的中点.
的中点.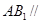 平面
平面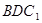 ;
;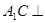 平面
平面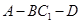 的正切值.
的正切值.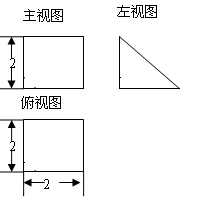
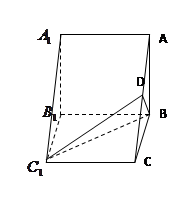
 中,
中, ,
, 为
为 中点,
中点, 为
为 中点,侧面
中点,侧面 为正方形。
为正方形。 平面
平面 ;
; ;
;

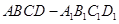 中,
中,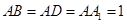 ,
, 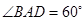 ,
,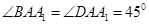 ,
,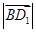 ;
;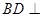 平面
平面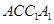 .
.