题目内容
(1)(参数方程)在极坐标系中,定点A(2,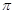 ),动点B在直线
),动点B在直线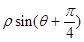 =
=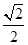 上运动,则线段AB的最短长度为 .
上运动,则线段AB的最短长度为 .
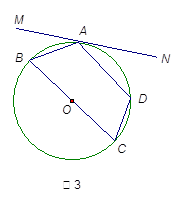
(2)(几何证明选讲)如图,在半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为 。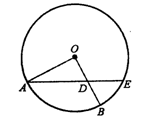
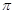 ),动点B在直线
),动点B在直线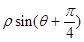 =
=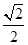 上运动,则线段AB的最短长度为 .
上运动,则线段AB的最短长度为 .(2)(几何证明选讲)如图,在半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为 。

(1)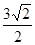 ;(2)
;(2)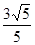
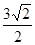 ;(2)
;(2)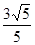
(1)A(2,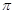 )化为直角坐标是(-2,0),直线
)化为直角坐标是(-2,0),直线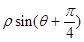 =
=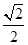 即
即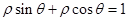 ,
,
化为直角坐标方程为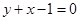 线段AB的最短长度为
线段AB的最短长度为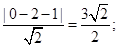
(2)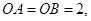 D为OB的中点,所以
D为OB的中点,所以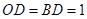 ,又∠AOB=90°,所以
,又∠AOB=90°,所以
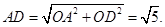 设BO延长线 交圆与F;则DF=3;由相交弦定理得:
设BO延长线 交圆与F;则DF=3;由相交弦定理得:
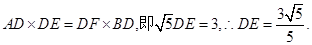
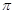 )化为直角坐标是(-2,0),直线
)化为直角坐标是(-2,0),直线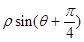 =
=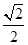 即
即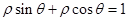 ,
,化为直角坐标方程为
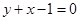 线段AB的最短长度为
线段AB的最短长度为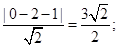
(2)
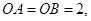 D为OB的中点,所以
D为OB的中点,所以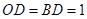 ,又∠AOB=90°,所以
,又∠AOB=90°,所以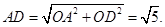 设BO延长线 交圆与F;则DF=3;由相交弦定理得:
设BO延长线 交圆与F;则DF=3;由相交弦定理得: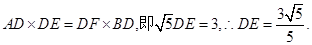

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
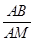 的值.
的值.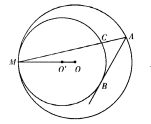
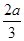 ,∠OAP=30°,则CP=_____
,∠OAP=30°,则CP=_____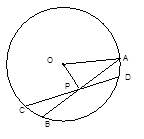
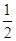 )=0
)=0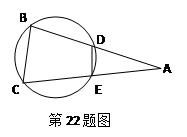
 ,C为
,C为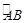 中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=
中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2= ,则OD+OE的取值范围是
,则OD+OE的取值范围是 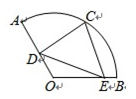

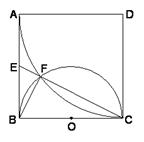
 是边长为
是边长为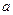 的正方形,以
的正方形,以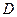 为圆心,
为圆心,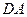 为半径的圆弧与以
为半径的圆弧与以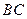 为直径的圆
为直径的圆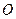 交于点
交于点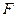 ,连接
,连接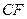 并延长
并延长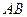 点
点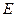
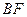 的长
的长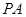 是圆
是圆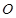 的切线,
的切线,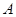 为切点,过
为切点,过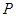 做圆
做圆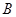 、
、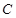 两点,
两点,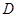 为弦
为弦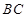 的中点,若圆心
的中点,若圆心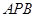 的内部,则∠
的内部,则∠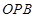 +∠
+∠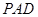 的度数为: ;
的度数为: ;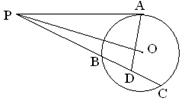
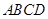 内接于⊙
内接于⊙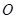 ,
,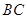 是直径,
是直径,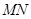 与
与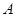 ,
,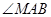
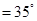 , 则
, 则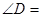 .
.