题目内容
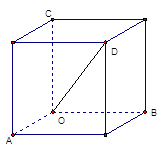
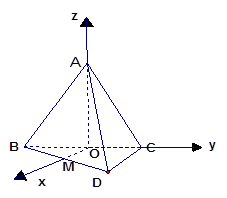
(本小题满分14分)如图,在三棱锥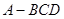 中,面
中,面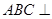 面
面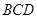 ,
,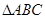 是正三角形,
是正三角形, 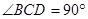 ,
,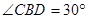 .
.
(Ⅰ)求证: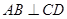 ;
;
(Ⅱ)求平面DAB与平面ABC的夹角的余弦值;
(Ⅲ)求异面直线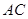 与
与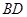 所成角的余弦值.
所成角的余弦值.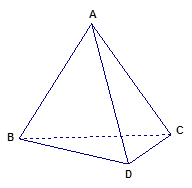
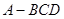 中,面
中,面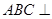 面
面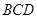 ,
,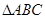 是正三角形,
是正三角形, 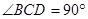 ,
,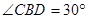 .
.(Ⅰ)求证:
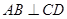 ;
;(Ⅱ)求平面DAB与平面ABC的夹角的余弦值;
(Ⅲ)求异面直线
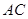 与
与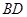 所成角的余弦值.
所成角的余弦值.
(Ⅰ)见解析;(Ⅱ) 平面DAB与平面ABC的夹角的余弦值为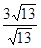 ;
;
(Ⅲ)异面直线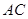 与
与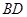 所成角的余弦值为
所成角的余弦值为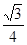 。
。
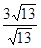 ;
;(Ⅲ)异面直线
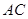 与
与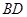 所成角的余弦值为
所成角的余弦值为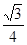 。
。本试题主要是考查了线线的垂直和二面角的求解,以及异面直线的所成的角的求解的综合运用。
(1)先根据线面垂直的性质定理得到线线垂直的判定。
(2)要求解二面角的平面角可以运用三垂线定理作出角,或者利用空间向量表示的二面角平面角。
(3)对于异面直线的所成的角,可以通过平移法得到结论。
(Ⅰ)分别取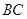 、
、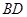 的中点
的中点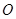 、
、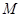 ,连结
,连结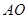 、
、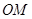 .
.
∵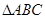 是正三角形,∴
是正三角形,∴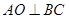 .
.
∵面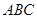 ⊥面
⊥面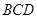 ,且面
,且面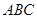
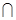 面
面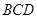
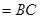 ,
,
∴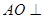 平面
平面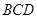 .∵
.∵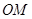 是
是 的中位线,且
的中位线,且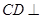 平面
平面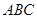 ,∴
,∴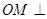 平面
平面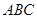 .
.
以点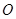 为原点,
为原点,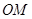 所在直线为
所在直线为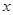 轴,
轴,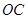 所
所
在直线为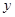 轴,
轴,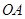 所在直线为
所在直线为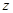 轴,建立空间直角坐标系.设
轴,建立空间直角坐标系.设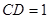 ,则
,则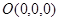 ,
,
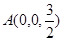 ,
,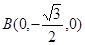 ,
, 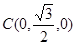 ,
,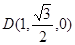 .
.
∴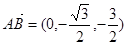 ,
,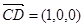 . ……………………2分
. ……………………2分
∴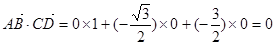 .
.
∴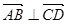 ,即
,即 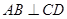 . …………………5分
. …………………5分
(Ⅱ)∵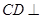 平面
平面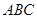 , ∴平面
, ∴平面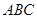 的法向量为
的法向量为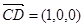 .
.
设平面 的法向量为
的法向量为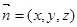 ,∴
,∴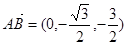 ,
,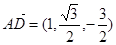 .
.
∴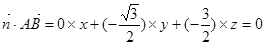 ,即
,即 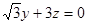 .
.
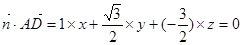 ,即
,即 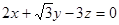 .
.
∴令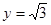 ,则
,则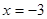 ,
,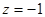 . ∴
. ∴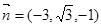 .
.
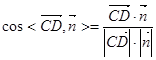
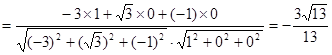 .
.
平面DAB与平面ABC的夹角的余弦值为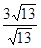 …………………10分
…………………10分
(Ⅲ)∵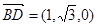 ,
,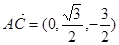 ,
,
∴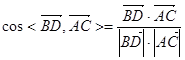
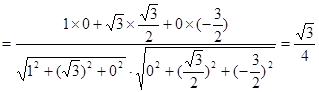 .
.
∴异面直线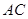 与
与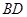 所成角的余弦值为
所成角的余弦值为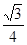 …………………14
…………………14
(1)先根据线面垂直的性质定理得到线线垂直的判定。
(2)要求解二面角的平面角可以运用三垂线定理作出角,或者利用空间向量表示的二面角平面角。
(3)对于异面直线的所成的角,可以通过平移法得到结论。
(Ⅰ)分别取
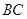 、
、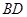 的中点
的中点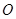 、
、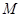 ,连结
,连结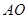 、
、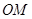 .
.∵
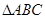 是正三角形,∴
是正三角形,∴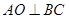 .
.∵面
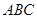 ⊥面
⊥面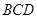 ,且面
,且面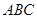
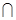 面
面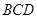
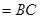 ,
,∴
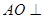 平面
平面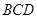 .∵
.∵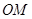 是
是 的中位线,且
的中位线,且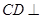 平面
平面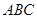 ,∴
,∴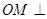 平面
平面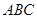 .
.以点
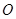 为原点,
为原点,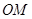 所在直线为
所在直线为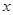 轴,
轴,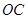 所
所 在直线为
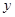 轴,
轴,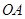 所在直线为
所在直线为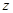 轴,建立空间直角坐标系.设
轴,建立空间直角坐标系.设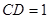 ,则
,则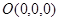 ,
,
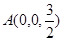 ,
,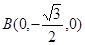 ,
, 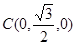 ,
,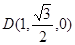 .
.∴
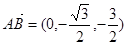 ,
,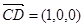 . ……………………2分
. ……………………2分∴
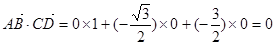 .
.∴
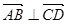 ,即
,即 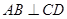 . …………………5分
. …………………5分(Ⅱ)∵
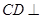 平面
平面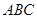 , ∴平面
, ∴平面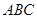 的法向量为
的法向量为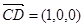 .
. 设平面
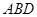 的法向量为
的法向量为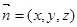 ,∴
,∴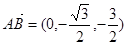 ,
,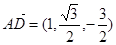 .
.∴
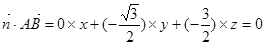 ,即
,即 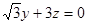 .
.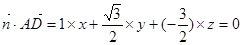 ,即
,即 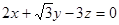 .
.∴令
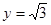 ,则
,则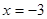 ,
,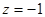 . ∴
. ∴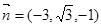 .
. 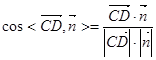
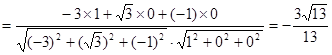 .
.平面DAB与平面ABC的夹角的余弦值为
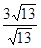 …………………10分
…………………10分(Ⅲ)∵
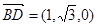 ,
,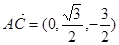 ,
,∴
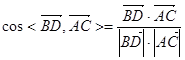
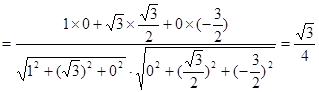 .
.∴异面直线
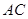 与
与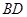 所成角的余弦值为
所成角的余弦值为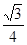 …………………14
…………………14
练习册系列答案
相关题目
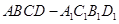 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱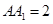 ,
,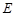 为
为 中点,
中点,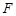 为
为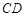 中点,
中点,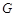 为
为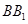 上一个动点.
上一个动点.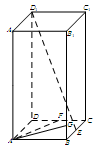
 ;
;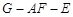 的平面角余弦值.
的平面角余弦值. 中,二面角
中,二面角 的余弦值为 .
的余弦值为 . 的侧面
的侧面 垂直于底面
垂直于底面 ,
, ,
, ,
, ,
, 在棱
在棱 上,
上, 是
是 的中点,二面角
的中点,二面角 为
为

 的值;
的值; 与平面
与平面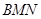 所成角的正弦值.
所成角的正弦值. ,则
,则 与
与 所成角为( )
所成角为( )



 所成的角为300,则它和平面
所成的角为300,则它和平面 与平面
与平面 所成的角为30°,
所成的角为30°, 为空间一定点,过
为空间一定点,过 ,则这样的直线
,则这样的直线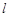 与这三条直线所成的角均为
与这三条直线所成的角均为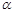 ,则
,则 .
.