题目内容
(14分)已知椭圆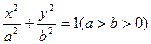 的两个焦点分别为F1(-c,0),F2(c
的两个焦点分别为F1(-c,0),F2(c ,0),(c>0),过点E
,0),(c>0),过点E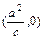 的直线与椭圆交于A、B两点,且F1A//F2B,|F1A|=2|F2B|,
的直线与椭圆交于A、B两点,且F1A//F2B,|F1A|=2|F2B|,
(1)求离心率;
( 2)求直线AB的斜率;
2)求直线AB的斜率;
(3)设点C与点A关于标标原点对称,直线F2B上有一点H(m,n)(m≠0)在△AF1C的外接圆上,求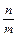 的值。
的值。
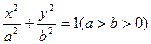 的两个焦点分别为F1(-c,0),F2(c
的两个焦点分别为F1(-c,0),F2(c ,0),(c>0),过点E
,0),(c>0),过点E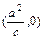 的直线与椭圆交于A、B两点,且F1A//F2B,|F1A|=2|F2B|,
的直线与椭圆交于A、B两点,且F1A//F2B,|F1A|=2|F2B|,(1)求离心率;
(
 2)求直线AB的斜率;
2)求直线AB的斜率;(3)设点C与点A关于标标原点对称,直线F2B上有一点H(m,n)(m≠0)在△AF1C的外接圆上,求
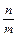 的值。
的值。(1)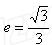 (2)
(2) (3)
(3)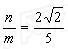
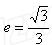 (2)
(2) (3)
(3)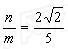
由F1A//F2B且|F1A|=2|F2B|

(2)b2=a2-c2=2c2
∴ 2x2+3y2=6c2
设直线AB: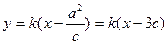 ,设A(x1,y1)、B(x2,y2)
,设A(x1,y1)、B(x2,y2)
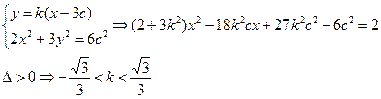
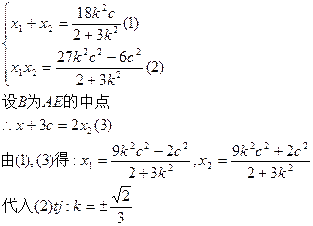
(3)由(2)知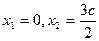 ,当
,当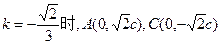
线段AF1的垂直分线l的方程:
直线l与x轴的交点为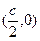 是△AF1C的外接圆的圆心,因此外接圆方程:
是△AF1C的外接圆的圆心,因此外接圆方程:
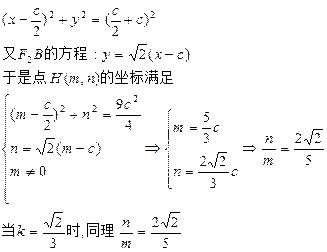

(2)b2=a2-c2=2c2
∴ 2x2+3y2=6c2
设直线AB:
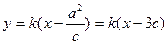 ,设A(x1,y1)、B(x2,y2)
,设A(x1,y1)、B(x2,y2)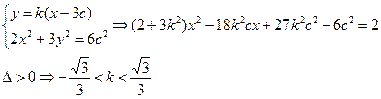
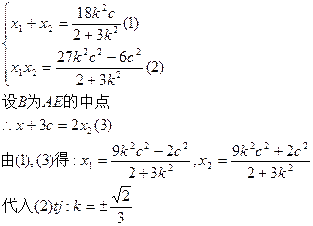
(3)由(2)知
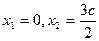 ,当
,当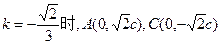
线段AF1的垂直分线l的方程:

直线l与x轴的交点为
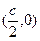 是△AF1C的外接圆的圆心,因此外接圆方程:
是△AF1C的外接圆的圆心,因此外接圆方程: 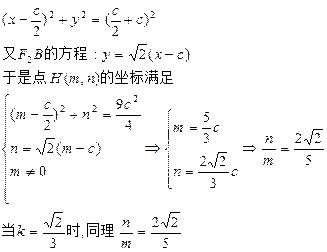

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
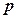 :“方程
:“方程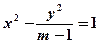 表示焦点在
表示焦点在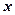 轴上的双曲线”,命题
轴上的双曲线”,命题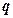 :“在区间
:“在区间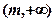 上,函数
上,函数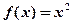 单调递增”,若
单调递增”,若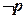 是真命题,
是真命题,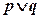 是真命题,求实数
是真命题,求实数 的取值范围。
的取值范围。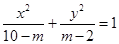 ,长轴在
,长轴在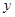 轴上. 若焦距为
轴上. 若焦距为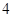 ,则
,则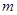 等于( )
等于( )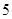 .
.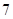 .
.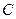 :
: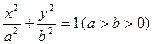 的离心率为
的离心率为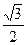 ,过坐标原点
,过坐标原点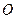 且斜率为
且斜率为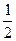 的直线
的直线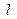 与
与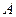 、
、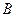 ,
,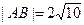 .
.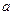 、
、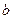 的值;
的值;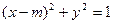 与椭圆
与椭圆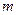 的取值范围.
的取值范围.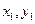 ),B(
),B(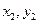 )是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离p(A,B)为
)是平面直角坐标系xOy上的两点,先定义由点A到点B的一种折线距离p(A,B)为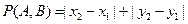 .
.
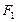 ,
,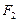 分别是双曲线
分别是双曲线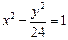 的左、右焦点,
的左、右焦点,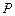 是双曲线上的一点,若
是双曲线上的一点,若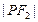 ,
,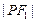 ,
,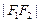 构成公差为正数的等差数列,则
构成公差为正数的等差数列,则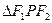 的面积为
的面积为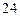
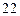
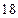
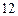
 的两个顶点为
的两个顶点为 ,
, ,
,



 的左
的左 、右焦点为F1、F2,其一条渐近线为y=x,点P
、右焦点为F1、F2,其一条渐近线为y=x,点P 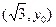 在该双曲线上,则
在该双曲线上,则 =( )
=( )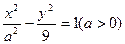 的一条渐近线方程为
的一条渐近线方程为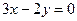 ,则
,则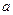 的值为 。
的值为 。