题目内容
不等式选讲已知函数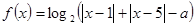 。
。
⑴当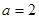 时,求函数
时,求函数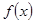 的最小值;
的最小值;
⑵当函数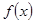 的定义域为
的定义域为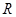 时,求实数
时,求实数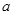 的取值范围。
的取值范围。
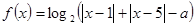 。
。⑴当
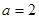 时,求函数
时,求函数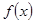 的最小值;
的最小值;⑵当函数
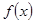 的定义域为
的定义域为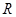 时,求实数
时,求实数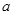 的取值范围。
的取值范围。(1)1(2)a<4
试题分析:解:(1)根据题意,由于
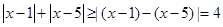
则可知当a=2时,有
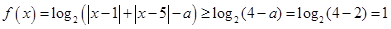
故可知
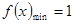 ..(5分)
..(5分)(2)因为当函数
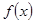 的定义域为
的定义域为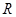 时,那么明真数鞥取遍一切的正实数,即可知,真数部分的最小值小于等于零即可,即
时,那么明真数鞥取遍一切的正实数,即可知,真数部分的最小值小于等于零即可,即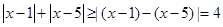 ,
,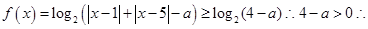 a<4 (10分)
a<4 (10分)点评:解决该试题的关键是对于绝对值符号的去掉,然后结合分段函数的性质来求解最值,以及参数的范围, 属于中档题

练习册系列答案
相关题目
 (
(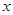 >0)取最小值时相应的
>0)取最小值时相应的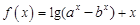 中,常数
中,常数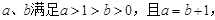 那么
那么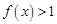 的解集为
的解集为
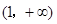
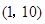
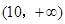
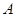 和
和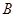 的含铁率
的含铁率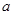 ,冶炼每万吨铁矿石的
,冶炼每万吨铁矿石的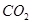 的排放量
的排放量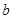 及每万吨铁矿石的价格
及每万吨铁矿石的价格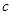 如下表:
如下表: (万吨),则购买铁矿石的最少费用为
(万吨),则购买铁矿石的最少费用为 (百万元).
(百万元).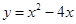 ,其中
,其中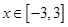 ,则该函数的值域为___________.
,则该函数的值域为___________.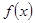 的定义域为实数集R,
的定义域为实数集R,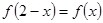 ,且当
,且当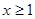 时,
时,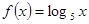 ,则有( )
,则有( )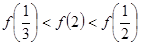
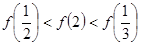
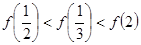
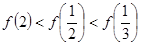
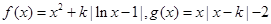 ,其中
,其中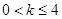 .(1) 讨论函数
.(1) 讨论函数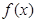 的单调性,并求出
的单调性,并求出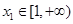 ,都存在
,都存在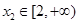 ,使得
,使得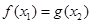 ,求实数
,求实数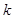 的取值范围.
的取值范围.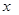 套世博吉祥物“海宝”所需成本费用为
套世博吉祥物“海宝”所需成本费用为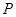 元,且
元,且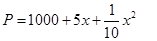 ,而每套“海宝”售出的价格为
,而每套“海宝”售出的价格为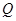 元,其中
元,其中
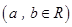 ,
,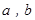 的值.(利润 = 销售收入-成本)
的值.(利润 = 销售收入-成本)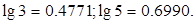 )
)