题目内容
2. 在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,$BA=\sqrt{2}$.
在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,$BA=\sqrt{2}$.(Ⅰ)求证:EF⊥平面BAC;
(Ⅱ)在线段AD上是否存在一点Q,使得AF∥平面BEQ?若存在,求二面角Q-BE-A的余弦值,若不存在,请说明理由.
分析 (Ⅰ)取AB中点H,连结DH、HF,证明DH⊥平面ABC,证明EF∥DH,然后证明EF⊥平面ABC;
(Ⅱ)以D为原点建立如图所示空间直角坐标系D-xyz.求出平面BQE的法向量,平面BAE的法向量,利用二面角Q-BE-A为锐二面角,通过向量的数量积求解即可.
解答 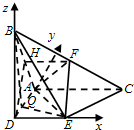 解:(Ⅰ)证明:取AB中点H,连结DH、HF,
解:(Ⅰ)证明:取AB中点H,连结DH、HF,
因为在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,D、E分别是边AB、BC的中点,所以AD=BD=1,
又因为翻折后$AB=\sqrt{2}$,所以翻折后AD⊥BD,且△ADB
为等腰直角三角形,所以DH⊥AB,
因为翻折后DE⊥AD,DE⊥BD,且AD∩BD=D,∴DE⊥平面ADB,因为DE∥AC,
∴AC⊥平面ADB,∴AC⊥DH,又AB∩AC=A,∴DH⊥平面ABC,
又∵HF∥AC,DE∥AC,且$HF=\frac{1}{2}AC=DE$,∴DEFH是平行四边形,∴EF∥DH,
∴EF⊥平面ABC; …(5分)
(Ⅱ)以D为原点建立如图所示空间直角坐标系D-xyz.则A(0,1,0),B(0,0,1),E(1,0,0),C(2,1,0),$F(1,\frac{1}{2},\frac{1}{2})$,设Q(0,t,0)(0≤t≤1),
则$\overrightarrow{BQ}=(0,t,-1)$,$\overrightarrow{EQ}=(-1,t,0)$,$\overrightarrow{AF}=(1,-\frac{1}{2},\frac{1}{2})$,
设平面BQE的法向量为$\overrightarrow n=(x,y,z)$,则由$\overrightarrow n•\overrightarrow{BQ}=0$,且$\overrightarrow n•\overrightarrow{EQ}=0$,得$\left\{\begin{array}{l}yt-x=0\\-x+ty=0\end{array}\right.$,
取y=1,则$\overrightarrow{n}=(t,1,t)$,
要使AF∥平面BEQ,则须$\overrightarrow{n}•\overrightarrow{AF}$=$(t,1,t)(1,-\frac{1}{2},\frac{1}{2})$=$t-\frac{1}{2}+\frac{1}{2}t=0$,
所以$t=\frac{1}{3}$,即线段AD上存在一点$Q(0,\frac{1}{3},0)$,使得AF∥平面BEQ,…(9分)
设平面BAE的法向量为$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$,则由$\overrightarrow{n_1}•\overrightarrow{AB}=0$,且${\overrightarrow n_1}•\overrightarrow{AE}=0$,得$\left\{\begin{array}{l}-{y_1}+{z_1}=0\\{x_1}-{y_1}=0\end{array}\right.$,
取y1=1,则$\overrightarrow{n_1}=(1,1,1)$,∴$cos<\overrightarrow n,\overrightarrow{n_1}>=\frac{{\frac{1}{3}+1+\frac{1}{3}}}{{\sqrt{\frac{11}{9}}•\sqrt{3}}}=\frac{5}{{\sqrt{33}}}=\frac{{5\sqrt{33}}}{33}$,
因为二面角Q-BE-A为锐二面角,所以其余弦值为$\frac{{5\sqrt{33}}}{33}$,
即线段AD上存在一点Q(点Q是线段AD上的靠近点D的一个三等分点),
使得AF∥平面BEQ,此时二面角Q-BE-A的余弦值为$\frac{{5\sqrt{33}}}{33}$…(12分)
点评 本题考查二面角的平面角的求法,直线与平面平行与垂直的判定定理的应用,考查空间想象能力以及计算能力.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | y2=8x | B. | y2=$\frac{{16\sqrt{3}}}{3}$x | C. | y2=$\frac{{8\sqrt{3}}}{3}$x | D. | y2=16x |
| A. | $\sqrt{5}$ | B. | 4 | C. | $\sqrt{13}$ | D. | $\sqrt{17}$ |