题目内容
14.如果双曲线x2-y2=a2经过圆(x-3)2+(y-1)2=5的直径AB的两个端点,则正实数a的值等于2.分析 设点,代入作差,可得AB的方程为y=3x-8,与圆方程联立,利用a2=(x+y)(x-y)=(4x-8)(8-2x)=8-8(x-3)2,即可求出正实数a的值.
解答 解:设A(x1,y1),B(x2,y2),代入双曲线方程作差得(x1+x2)(x1-x2)=(y1+y2)(y1-y2),
∵x1+x2=6,y1+y2=2,$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$=3,
∴AB的方程为y=3x-8,与圆方程联立得10(x-3)2=5,
∴(x-3)2=$\frac{1}{2}$,
∴a2=(x+y)(x-y)=(4x-8)(8-2x)=8-8(x-3)2=4.
∴a=2.
故答案为:2.
点评 本题考查双曲线的方程与性质,考查点差法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.若非零向量$\overrightarrow a,\overrightarrow b$满足($\overrightarrow{a}$-4$\overrightarrow{b}$)⊥$\overline{a}$,($\overrightarrow{b}$-$\overrightarrow{a}$)⊥$\overrightarrow{b}$,则$\overrightarrow a$与$\overrightarrow b$的夹角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{5π}{6}$ |
19.已知集合A={x|-1<x<1},B={x|x2-3x≤0},则A∩B等于( )
| A. | [-1,0] | B. | (-1,3] | C. | [0,1) | D. | {-1,3} |
3.要得到一个偶函数,只需将f(x)=sin2x的图象( )
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向左平移π个单位 |
 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=$\sqrt{10}$,∠DBC=45°
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=$\sqrt{10}$,∠DBC=45° 在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,$BA=\sqrt{2}$.
在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,$BA=\sqrt{2}$.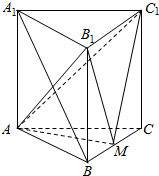 如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形. 为了调查高一新生中女生的体重情况,校卫生室随机选取20名女生作为样本测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(55,60]上的女生数之比为4:3.
为了调查高一新生中女生的体重情况,校卫生室随机选取20名女生作为样本测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(55,60]上的女生数之比为4:3.