题目内容
17.已知函数f(x)=ex-lnx,g(x)=ex-1+a-lnx,其中e=2.71828…,a∈R.(1)求f(x)的零点;
(2)求g(x)的极值;
(3)如果s,t,r满足|s-r|<|t-r|,那么称s比t更靠近r.当a≥2且x≥1时,试比较ex和ex-1+a哪个更靠近lnx,并说明理由.
分析 (1)求出函数的导数,得到当0<x≤e时,f(x)≥0;当x>e时,f(x)<0,即可求f(x)的零点;
(2)求出函数的导数,确定x∈(0,1)时,g'(x)<0,g(x)递减,当x∈(1,+∞)时,g'(x)>0,g(x)递增,即可求g(x)的极值;
(3)当1≤x≤e时,推出|f(x)|<|g(x)|,说明ex比ex-1+a更靠近lnx.当x>e时,通过作差,构造新函数,利用二次求导,判断函数的单调性,证明ex比ex-1+a更靠近lnx.
解答 解:(1)∵f(x)=ex-lnx,∴f′(x)=-ex2-1x,
∴f(x)=ex-lnx在(0,+∞)上是减函数,又f(e)=0
∴当0<x≤e时,f(x)≥0;当x>e时,f(x)<0.
∴x=e是f(x)的唯一零点.…(3分)
(2)∵g(x)=ex-1+a-lnx,∴g′(x)=ex−1−1x,g″(x)=ex-1+1x2>0,
∴g'(x)在(0,+∞)上为增函数,又g'(1)=0,
∴x∈(0,1)时,g'(x)<0,g(x)递减,当x∈(1,+∞)时,g'(x)>0,g(x)递增
∴x=1为g(x)的极小值点,极小值为g(1)=a+1,g(x)无极大值.…(6分)
(3)当1≤x≤e时,|f(x)|-|g(x)|=ex-ex-1-a
设m(x)=ex-ex-1-a,则m′(x)=−ex2−ex−1<0,∴m(x)在[1,+∞)上为减函数
∴m(x)≤m(1)=e-1-a,∵a≥2,∴m(x)<0,
∴|f(x)|<|g(x)|,∴ex比ex-1+a更靠近lnx…(9分)
当x>e时,|f(x)|−|g(x)|=−f(x)−g(x)=−ex+2lnx−ex−1−a<2lnx−ex−1−a
设n(x)=2lnx-ex-1-a,则n′(x)=2x−ex−1,n″(x)=-2x2−ex−1<0
∴n'(x)在(e,+∞)上为减函数,∴n′(x)<n′(e)=2e−ee−1<0,
∴n(x)在(e,+∞)上为减函数,∴n(x)<n(e)=2-a-ee-1<0,∴|f(x)|<|g(x)|
∴ex比ex-1+a更靠近lnx…(12分)
综上,在a≥2,x≥1时,ex比ex-1+a更靠近lnx.…(14分)
点评 本小题主要考查函数与导数的综合应用能力,具体涉及到用导数来描述函数的单调性等情况.本小题主要考查考生分类讨论思想的应用,对考生的逻辑推理能力与运算求解有较高要求.

 阅读快车系列答案
阅读快车系列答案| A. | \frac{π}{6} | B. | \frac{π}{3} | C. | \frac{π}{2} | D. | \frac{5π}{6} |
| A. | 3 | B. | 4 | C. | log310+3 | D. | 5 |
 在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,
在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,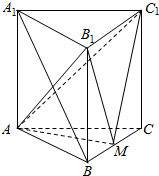 如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,直三棱柱ABC-A1B1C1的底面是边长为A的正三角形,点M在边BC上,△AMC1是以M为直角顶点的等腰直角三角形. 为了调查高一新生中女生的体重情况,校卫生室随机选取20名女生作为样本测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(55,60]上的女生数之比为4:3.
为了调查高一新生中女生的体重情况,校卫生室随机选取20名女生作为样本测量她们的体重(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中体重在区间(45,50]上的女生数与体重在区间(55,60]上的女生数之比为4:3.