题目内容
【题目】每年的4月23日为世界读书日，为调查某高校学生（学生很多）的读书情况，随机抽取了男生，女生各20人组成的一个样本，对他们的年阅读量（单位：本）进行了统计，分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图． 男生年阅读量的频率分布表（年阅读量均在区间[0，60]内）：
本/年 | [0，10） | [10，20） | [20，30） | [30，40） | [40，50） | [50，60] |
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
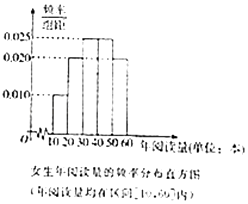
（1）根据女生的频率分布直方图估计该校女生年阅读量的中位数；
（2）在样本中，利用分层抽样的方法，从男生年与度量在[20，30），[30，40）的两组里抽取6人，再从这6人中随机抽取2人，求[30，40）这一组中至少有1人被抽中的概率；
（3）若年阅读量不小于40本为阅读丰富，否则为阅读不丰富，依据上述样本研究阅读丰富与性别的关系，完成下列2×2列联表，并判断是否有99%的把握认为月底丰富与性别有关．
性别 阅读量 | 丰富 | 不丰富 | 合计 |
男 | |||
女 | |||
合计 |
P（K2≥k0） | 0.025 | 0.010 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
附：K2= 
，其中n=a+b+c+d．
【答案】
（1）解：前三组频率之和为0.1+0.2+0.25=0.55，
∴中位数位于第三组，设中位数为a，则 
= 
，
∴a=38，
∴估计该校女生年阅读量的中位数为38；
（2）解：利用分层抽样的方法，从男生年与度量在[20，30），[30，40）的两组里抽取6人，从这6人中随机抽取2人，共有方法 
=15种，各组分别为4人，2人，[30，40）这一组中至少有1人被抽中的概率1﹣ 
= 
；
（3）解：
性别 阅读量 | 丰富 | 不丰富 | 合计 |
男 | 4 | 16 | 20 |
女 | 9 | 11 | 20 |
合计 | 13 | 27 | 40 |
K2= 
≈2.849＜6.635，
∴没有99%的把握认为月底丰富与性别有关
【解析】（1）求出前三组频率之和，即可根据女生的频率分布直方图估计该校女生年阅读量的中位数；（2）确定基本事件的个数，即可求[30，40）这一组中至少有1人被抽中的概率；（3）根据所给数据得出2×2列联表，求出K2 ， 即可判断是否有99%的把握认为月底丰富与性别有关．
