题目内容
【题目】如图,在三棱锥![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点.已知
的中点.已知![]() ,
,![]() .
.

求证:(1)直线PA![]() 平面DEF;
平面DEF;
(2)平面BDE⊥平面ABC.
【答案】(1)见解析(2)见解析
【解析】
试题分析:(1) 由线面平行的判定定理可知,只须证PA与平面DEF内的某一条直线平行即可,由已知及图形可知应选择DE,由三角形的中位线的性质易知: DE∥PA ,从而问题得证;注意线PA在平面DEG外,而DE在平面DEF内必须写清楚;(2) 由面面垂直的判定定理可知,只须证两平中的某一直线与另一个平面垂直即可,注意题中已知了线段的长度,那就要注意利用勾股定理的逆定理来证明直线与直线的垂直;通过观察可知:应选择证DE垂直平面ABC较好,由(1)可知:DE⊥AC,再就只须证DE⊥EF即可;这样就能得到DE⊥平面ABC,又DE![]() 平面BDE,从面而有平面BDE⊥平面ABC.
平面BDE,从面而有平面BDE⊥平面ABC.
试题解析:(1)因为D,E分别为PC,AC的中点,所以DE∥PA.
又因为PA![]() 平面DEF,DE
平面DEF,DE![]() 平面DEF,所以直线PA∥平面DEF.
平面DEF,所以直线PA∥平面DEF.
(2)因为D,E,F分别人棱PC,AC,AB的中点,PA=6,BC=8,所以DE∥PA,DE=![]() PA=3,EF=
PA=3,EF=![]() BC=4.
BC=4.
又因为DF=5,故DF2=DE2+EF2,所以∠DEF=90。,即DE⊥EF.又PA⊥AC,DE∥PA,所以DE⊥AC.
因为AC∩EF=E,AC![]() 平面ABC,EF
平面ABC,EF![]() 平面ABC,所以DE⊥平面ABC.
平面ABC,所以DE⊥平面ABC.
又DE![]() 平面BDE,所以平面BDE⊥平面ABC.
平面BDE,所以平面BDE⊥平面ABC.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案【题目】每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图. 男生年阅读量的频率分布表(年阅读量均在区间[0,60]内):
本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
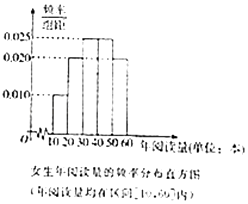
(1)根据女生的频率分布直方图估计该校女生年阅读量的中位数;
(2)在样本中,利用分层抽样的方法,从男生年与度量在[20,30),[30,40)的两组里抽取6人,再从这6人中随机抽取2人,求[30,40)这一组中至少有1人被抽中的概率;
(3)若年阅读量不小于40本为阅读丰富,否则为阅读不丰富,依据上述样本研究阅读丰富与性别的关系,完成下列2×2列联表,并判断是否有99%的把握认为月底丰富与性别有关.
性别 阅读量 | 丰富 | 不丰富 | 合计 |
男 | |||
女 | |||
合计 |
P(K2≥k0) | 0.025 | 0.010 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
附:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.