题目内容
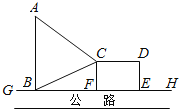
【题目】如图，
是东西方向的公路北侧的边缘线，某公司准备在上的一点
的正北方向的
处建一仓库，并在公路同侧建造一个正方形无顶中转站
（其中边
在上），现从仓库向和中转站分别修两条道路
，
，已知
，且
，设
，
．
（1）求
关于
的函数解析式；
（2）如果中转站四周围墙（即正方形周长）造价为
万元
，两条道路造价为
万元，问：取何值时，该公司建中转围墙和两条道路总造价
最低？
【答案】（1）
；（2）
的值为
时，该公司建中转站围墙和道路总造价
最低.
【解析】分析：（1）根据题意得
，在
中，
，然后在
中利用余弦定理建立关于
的等式，进而得到
关于的函数解析式；
（2）由（1）求出的函数关系式，结合题意得出总造价
，令
，化简得
，利用基本不等式，即可求解.
详解：（1）∵
，
，
∴
∵在中，
，
，
∴
，可得
由于
，得
在中，根据余弦定理
，
可得
，
即
，解得：
∵
且
∴
可得关于的函数解析式为
．
（2）由题意，可得总造价
令
，则
当且仅当
，即
时，M的最小值为49
此时
，
答：当的值为时，该公司建中转站围墙和道路总造价最低．
怎样学好牛津英语系列答案
【题目】每年的4月23日为世界读书日，为调查某高校学生（学生很多）的读书情况，随机抽取了男生，女生各20人组成的一个样本，对他们的年阅读量（单位：本）进行了统计，分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图． 男生年阅读量的频率分布表（年阅读量均在区间[0，60]内）：
本/年 | [0，10） | [10，20） | [20，30） | [30，40） | [40，50） | [50，60] |
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
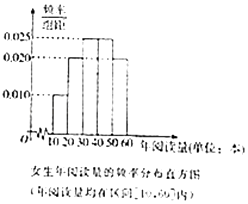
（1）根据女生的频率分布直方图估计该校女生年阅读量的中位数；
（2）在样本中，利用分层抽样的方法，从男生年与度量在[20，30），[30，40）的两组里抽取6人，再从这6人中随机抽取2人，求[30，40）这一组中至少有1人被抽中的概率；
（3）若年阅读量不小于40本为阅读丰富，否则为阅读不丰富，依据上述样本研究阅读丰富与性别的关系，完成下列2×2列联表，并判断是否有99%的把握认为月底丰富与性别有关．
性别 阅读量 | 丰富 | 不丰富 | 合计 |
男 | |||
女 | |||
合计 |
P（K2≥k0） | 0.025 | 0.010 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
附：K2= 
，其中n=a+b+c+d．
