题目内容
【题目】如图所示,三棱锥P﹣ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA= ![]() ,PB=
,PB= ![]() ,则三棱锥P﹣ABC的外接球的表面积为 .
,则三棱锥P﹣ABC的外接球的表面积为 . 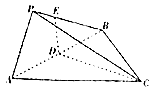
【答案】13π
【解析】解:由题意,PA2+PB2=AB2 , 因为 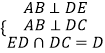 ,∴AD⊥面DEC, ∵ADPAB,ADABC,∴面APB⊥面DEC,面ABC⊥面DEC,
,∴AD⊥面DEC, ∵ADPAB,ADABC,∴面APB⊥面DEC,面ABC⊥面DEC,
在CD上取点O1 , 使O1为等边三角形ABC的中心,
∵D为△PAB斜边中点,∴在△DEC中,过D作直线与DE垂直,过O1作直线与DC垂直,两条垂线交于点O,则O为球心.
∵∠EDC=90°,∴ ![]() ,
,
又∵ ![]() ,∴OO1=
,∴OO1= ![]() ,三棱锥P﹣ABC的外接球的半径R=
,三棱锥P﹣ABC的外接球的半径R= ![]() ,
,
三棱锥P﹣ABC的外接球的表面积为4πR2=13π,
所以答案是:13π.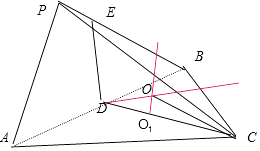
【考点精析】利用球内接多面体对题目进行判断即可得到答案,需要熟知球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长.

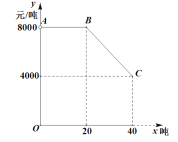
【题目】每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频率分布表和女生阅读量的频率分布直方图. 男生年阅读量的频率分布表(年阅读量均在区间[0,60]内):
本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
频数 | 3 | 1 | 8 | 4 | 2 | 2 |
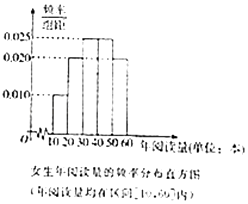
(1)根据女生的频率分布直方图估计该校女生年阅读量的中位数;
(2)在样本中,利用分层抽样的方法,从男生年与度量在[20,30),[30,40)的两组里抽取6人,再从这6人中随机抽取2人,求[30,40)这一组中至少有1人被抽中的概率;
(3)若年阅读量不小于40本为阅读丰富,否则为阅读不丰富,依据上述样本研究阅读丰富与性别的关系,完成下列2×2列联表,并判断是否有99%的把握认为月底丰富与性别有关.
性别 阅读量 | 丰富 | 不丰富 | 合计 |
男 | |||
女 | |||
合计 |
P(K2≥k0) | 0.025 | 0.010 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
附:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.