题目内容
【题目】设复数z=(x﹣1)+yi(x∈R,y≥0),若|z|≤1,则y≥x的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵复数z=(x﹣1)+yi(x,y∈R)且|z|≤1, ∴|z|= ![]() ≤1,即(x﹣1)2+y2≤1,
≤1,即(x﹣1)2+y2≤1,
∴点(x,y)在(1,0)为圆心1为半径的圆及其内部,
而y≥x表示直线y=x左上方的部分,(图中阴影弓形)
∴所求概率为弓形的面积与圆的面积一半的之比,
∴所求概率P= 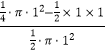 =
= ![]() ﹣
﹣ ![]()
故选:C.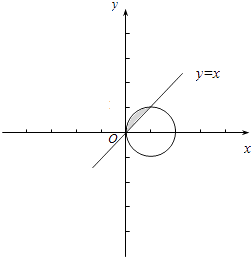
【考点精析】认真审题,首先需要了解复数的模(绝对值)(复平面内复数所对应的点到原点的距离,是非负数,因而两复数的模可以比较大小;复数模的性质:(1)![]() (2)
(2)![]() (3)若
(3)若![]() 为虚数,则
为虚数,则![]() ),还要掌握几何概型(几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等)的相关知识才是答题的关键.
),还要掌握几何概型(几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等)的相关知识才是答题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
