Question

【题目】解答题
（1）求不等式a2x﹣1＞ax+2（a＞0，且a≠1）中x的取值范围（用集合表示）．
（2）已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）= +1，求函数f（x）的解析式．

Answer 1

【答案】
（1）解：不等式a2x﹣1＞ax+2（a＞0，且a≠1），

∵当a＞1时，2x﹣1＞x+2，即x＞3．

当0＜a＜1时，2x﹣1＜x+2，即x＜3．

故不等式a2x﹣1＞ax+2（a＞0，且a≠1）的解集：

当a＞1时，{x|x＞3}，

当0＜a＜1时，{x|x＜3}

（2）解：已知f（x）是定义在R上的奇函数，f（﹣x）=﹣f（x），f（0）=0；

当x＞0时，f（x）= +1，

当x＜0时，则﹣x＞0，

故得f（﹣x）= +1，

∵f（x）是奇函数，∴f（﹣x）=﹣f（x），即﹣f（x）= +1，

∴f（x）=﹣ ﹣1，

∵f（x）是奇函数，∴f（0）=0，

∴f（x）=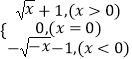

【解析】（1）根据指数函数的性质，求底数a进行讨论，求解不等式．（2）函数f（x）是定义在R上的奇函数，f（﹣x）=﹣f（x），当x＞0时，f（x）= +1，可求函数f（x）的解析式．