题目内容
【题目】已知正方体ABCD﹣A1B1C1D1 , O是底ABCD对角线的交点.求证: 
(1)C1O∥面AB1D1;
(2)平面A1AC⊥面AB1D1 .
【答案】
(1)证明:连结A1C1,设A1C1∩B1D1=O1,
连结AO1,因为ABCD﹣A1B1C1D1是正方体∴A1ACC1是平行四边形
∴AC∥A1C1且 AC=A1C1.
又O,O1分别是AC,A1C1的中点,∴O1C1∥AO且O1C1=AO,
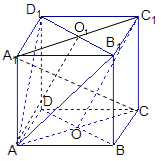
∴O1C1AO是平行四边形
∴OC1∥AO1,AO1面AB1D1,O1C面AB1D1
∴C1O∥面AB1D1.
(2)证明:∵CC1⊥面A1B1C1D1,∴CC1⊥B1D1,
又∵A1C1⊥B1D1,∴B1D1⊥面A1C1C,
即A1C⊥B1D1,
同理可证A1C⊥AB1,
又AB1∩B1D1=B1,
∴A1C⊥面AB1D1,
∴平面A1AC⊥面AB1D1.
【解析】(1)连结A1C1 , 设A1C1∩B1D1=O1 , 连结AO1 , 证明OC1∥AO1 , 然后证明C1O∥面AB1D1 . (2)证明A1C⊥B1D1 , A1C⊥AB1 , 推出A1C⊥面AB1D1 , 即可证明平面A1AC⊥面AB1D1 .
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.

【题目】(12分)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
甲班 | 6 | 5 | 7 | 9 | 8 |
乙班 | 4 | 8 | 9 | 7 | 7 |
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作![]() 和
和![]() ,试求
,试求![]() 和
和![]() 的分布列和数学期望.
的分布列和数学期望.
