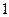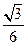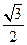题目内容
如图,在矩形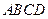 中,
中,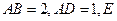 是
是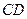 的中点,以
的中点,以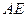 为折痕将
为折痕将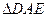 向上折起,使
向上折起,使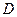 为
为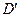 ,且平面
,且平面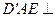 平面
平面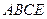 .
.
(Ⅰ)求证: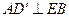 ;
;
(Ⅱ)求直线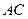 与平面
与平面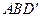 所成角的正弦值.
所成角的正弦值.
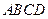 中,
中,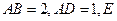 是
是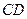 的中点,以
的中点,以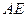 为折痕将
为折痕将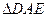 向上折起,使
向上折起,使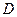 为
为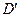 ,且平面
,且平面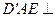 平面
平面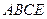 .
.(Ⅰ)求证:
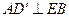 ;
;(Ⅱ)求直线
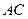 与平面
与平面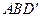 所成角的正弦值.
所成角的正弦值.
(1)略
(2)

(Ⅰ)在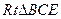 中,
中, ,
,

在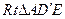 中,
中, ,
,
∵ ,∴
,∴ .…………………………………………..2分
.…………………………………………..2分
∵平面 平面
平面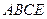 ,且交线为
,且交线为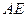 ,
,
∴ 平面
平面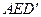 .
.
∵ 平面
平面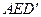 ,∴
,∴ .………………………………………………6分
.………………………………………………6分
(Ⅱ )(法一)设
)(法一)设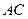 与
与 相交于点
相交于点 ,由(Ⅰ)知
,由(Ⅰ)知 ,
,
∵ ,∴
,∴ 平面
平面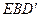 ,
,
∵ 平面
平面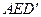 ,∴平面
,∴平面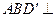 平面
平面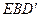 ,且交线为
,且交线为 ,……………………………………7分
,……………………………………7分
如图19-2,作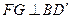 ,垂足为
,垂足为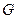 ,则
,则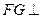 平面
平面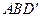 ,连
,连 结
结 ,则
,则 是直
是直 线
线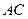 与平面
与平面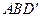 所成的角.…………………………………………..9分
所成的角.…………………………………………..9分
由平面几何的知识可知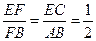 ,∴
,∴ .
.
在 中,
中, ,
,
在中,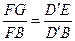 ,可求得
,可求得 .∴
.∴ 。
。
所以直线与平面所成角的正弦值为 。
。 …………………………………………..14分
…………………………………………..14分
(法二)向量法(略)
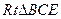 中,
中, ,
,
在
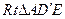 中,
中, ,
,∵
 ,∴
,∴ .…………………………………………..2分
.…………………………………………..2分∵平面
 平面
平面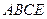 ,且交线为
,且交线为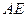 ,
,∴
 平面
平面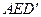 .
.∵
 平面
平面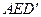 ,∴
,∴ .………………………………………………6分
.………………………………………………6分(Ⅱ
 )(法一)设
)(法一)设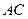 与
与 相交于点
相交于点 ,由(Ⅰ)知
,由(Ⅰ)知 ,
,∵
 ,∴
,∴ 平面
平面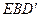 ,
,∵
 平面
平面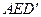 ,∴平面
,∴平面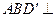 平面
平面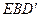 ,且交线为
,且交线为 ,……………………………………7分
,……………………………………7分如图19-2,作
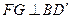 ,垂足为
,垂足为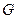 ,则
,则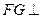 平面
平面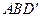 ,连
,连 结
结 ,则
,则 是直
是直 线
线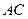 与平面
与平面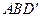 所成的角.…………………………………………..9分
所成的角.…………………………………………..9分由平面几何的知识可知
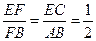 ,∴
,∴ .
. 在
 中,
中, ,
,在中,
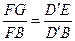 ,可求得
,可求得 .∴
.∴ 。
。所以直线与平面所成角的正弦值为
 。
。 …………………………………………..14分
…………………………………………..14分(法二)向量法(略)

练习册系列答案
 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
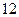 分)在边长为
分)在边长为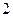 的正方体
的正方体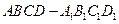 中,
中,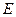 是
是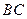 的中点,
的中点,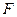 是
是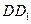 的中点,
的中点, 求证:
求证: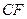 ∥
∥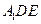 ;
;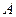 到平面
到平面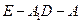 的平面角大小的余弦值.
的平面角大小的余弦值.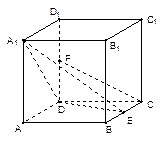
 CD垂直,已知BC=2AD=4,
CD垂直,已知BC=2AD=4,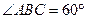 ,
,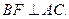
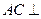 面ABF;
面ABF;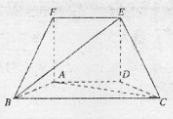
 三点A(0,2,3),B(-2,1,6),C(1,-1,5)
三点A(0,2,3),B(-2,1,6),C(1,-1,5)
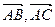 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;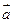 分别与向量
分别与向量 =
=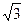 ,求向量
,求向量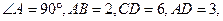 E为CD上一点,且DE=4,过E作EF//AD交BC于F现将
E为CD上一点,且DE=4,过E作EF//AD交BC于F现将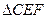 沿EF折到
沿EF折到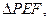 使
使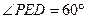 ,如图2。
,如图2。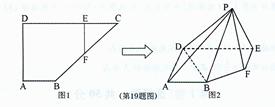
 ;
;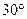 ?若存在,确定点M的位置;若不存在,请说明理由。
?若存在,确定点M的位置;若不存在,请说明理由。 经过A、B、C这三点的小圆周长为
经过A、B、C这三点的小圆周长为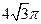 ,则球O的体积为 .
,则球O的体积为 .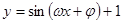 的一段图象如图所示,则它的一个周期T、初相
的一段图象如图所示,则它的一个周期T、初相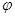 依次为( )
依次为( )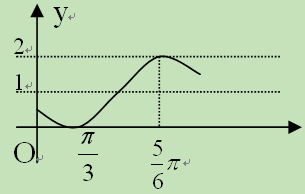
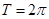 ,
,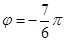
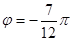
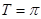 ,
, ,E、F分别为正方体的面
,E、F分别为正方体的面 、面
、面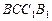 的中心,则四边形
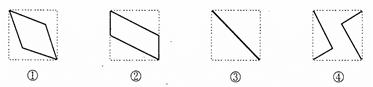
的中心,则四边形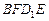 在该正方体的面上的射影可能是
在该正方体的面上的射影可能是 __________ (只写出序号即可)
__________ (只写出序号即可)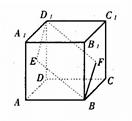
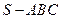 ,若空间一点
,若空间一点 满足
满足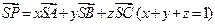 ,则
,则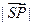 的最小值为
的最小值为