题目内容
(本小题满分12分)
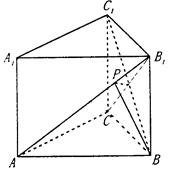
如图,正方形ADEF所在平面和等腰梯形所在平面AB CD垂直,已知BC=2AD=4,
CD垂直,已知BC=2AD=4,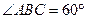 ,
,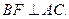
(I)求证: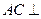 面ABF;
面ABF;
(II)求异面直线BE与AF所成的角;
(III)求该几何体的表面积。
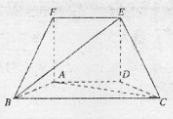
如图,正方形ADEF所在平面和等腰梯形所在平面AB
 CD垂直,已知BC=2AD=4,
CD垂直,已知BC=2AD=4,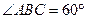 ,
,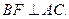
(I)求证:
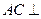 面ABF;
面ABF;(II)求异面直线BE与AF所成的角;
(III)求该几何体的表面积。

(1)略
(2)
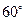
(3)
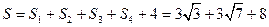
⑴证明:因为面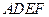
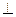 面
面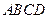 ,
,
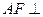 交线
交线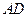 ,
,
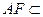 面
面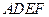 ,
,
所以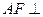 面
面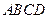 . ……2分
. ……2分
故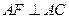 ,
,
又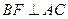 ,
,
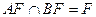 .
.
所以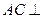 面
面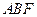 , ……4分
, ……4分
⑵解:注意到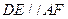 ,
,
所以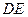 与
与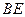 所成的角即为异面直线
所成的角即为异面直线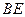 与
与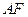 所成的角, ……6分
所成的角, ……6分
连接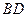 ,由⑴知
,由⑴知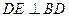 .
.
在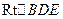 中,
中,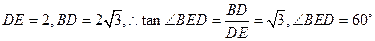 ,
,
异面直线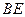 与
与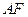 所成的角为
所成的角为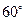 . ……
. …… 8分
8分
⑶解:由⑴知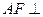 面
面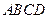 ,所以
,所以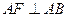 ,又
,又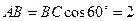 ,
,
所以△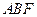 的面积
的面积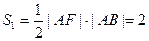 . ……9分
. ……9分
同理△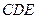 的面积
的面积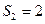 ,等腰梯形
,等腰梯形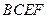 的上底长为
的上底长为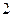 ,下底长为4,两腰长均为
,下底长为4,两腰长均为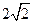 ,则它的高为
,则它的高为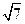 ,所以其面积
,所以其面积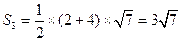 .……10分
.……10分
等腰梯形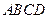 的上底长为
的上底长为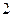 ,下底长为4,两腰长均为
,下底长为4,两腰长均为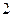 ,
,
则它的高为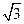 ,所以其面积
,所以其面积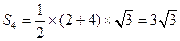 .…… 11分
.…… 11分
故该几何体的表面积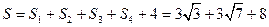 .…12分
.…12分
 面
面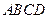 ,
,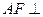 交线
交线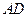 ,
,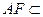 面
面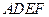 ,
,所以
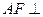 面
面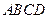 . ……2分
. ……2分故
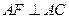 ,
,又
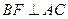 ,
,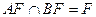 .
.所以
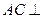 面
面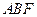 , ……4分
, ……4分⑵解:注意到
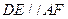 ,
,所以
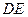 与
与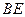 所成的角即为异面直线
所成的角即为异面直线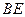 与
与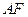 所成的角, ……6分
所成的角, ……6分连接
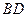 ,由⑴知
,由⑴知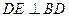 .
.在
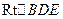 中,
中,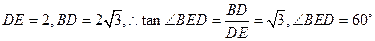 ,
,异面直线
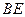 与
与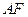 所成的角为
所成的角为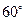 . ……
. …… 8分
8分⑶解:由⑴知
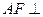 面
面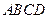 ,所以
,所以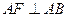 ,又
,又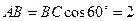 ,
,所以△
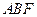 的面积
的面积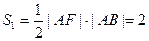 . ……9分
. ……9分同理△
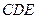 的面积
的面积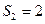 ,等腰梯形
,等腰梯形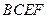 的上底长为
的上底长为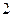 ,下底长为4,两腰长均为
,下底长为4,两腰长均为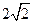 ,则它的高为
,则它的高为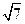 ,所以其面积
,所以其面积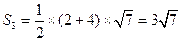 .……10分
.……10分等腰梯形
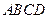 的上底长为
的上底长为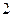 ,下底长为4,两腰长均为
,下底长为4,两腰长均为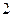 ,
,则它的高为
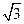 ,所以其面积
,所以其面积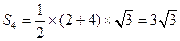 .…… 11分
.…… 11分故该几何体的表面积
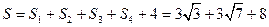 .…12分
.…12分
练习册系列答案
相关题目
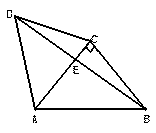
 中,
中,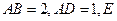 是
是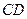 的中点,以
的中点,以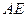 为折痕将
为折痕将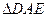 向上折起,使
向上折起,使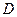 为
为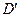 ,且平面
,且平面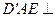 平面
平面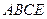 .
.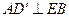 ;
;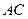 与平面
与平面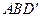 所成角的正弦值.
所成角的正弦值.
 的度数为
的度数为 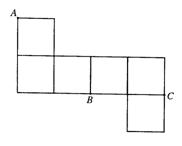
 和平面
和平面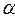 ,且
,且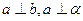 ,则
,则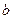 与
与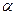 的位置关系是______________
的位置关系是______________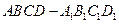 的底面
的底面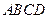 是菱形,
是菱形,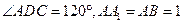 ,点
,点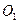 、
、 分别是上、下底面菱形的对角线的交点.⑴求证:
分别是上、下底面菱形的对角线的交点.⑴求证: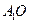 ∥平面
∥平面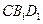 ;⑵求点
;⑵求点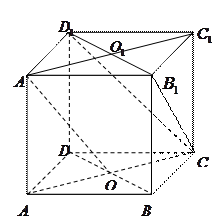
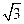 ,
,
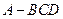 ,
,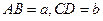 ,
, ,
,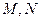 分别为
分别为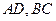 的中点,
的中点,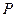 为
为 上一点,则
上一点,则 的最小值是
的最小值是