题目内容
4.函数y=2cos2(x-$\frac{π}{4}$)-1是①.①最小正周期为π的奇函数;
②最小正周期为π的偶函数;
③最小正周期为$\frac{π}{2}$的奇函数;
④最小正周期为$\frac{π}{2}$的偶函数.
分析 由条件利用二倍角的余弦公式化简函数的解析式,再利用正弦函数的周期性和奇偶性得出结论.
解答 解:函数y=2cos2(x-$\frac{π}{4}$)-1=cos(2x-$\frac{π}{2}$)=sin2x,
故函数是最小正周期为π的奇函数,
故答案为:①.
点评 本题主要考查二倍角的余弦公式,正弦函数的周期性和奇偶性,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
14.若不等式(-1)na<2+$\frac{(-1)^{n+1}}{n}$对于任意正整数n都成立,则实数a的取值范围是( )
| A. | $[-2,\frac{3}{2})$ | B. | $(-2,\frac{3}{2}]$ | C. | [-3,2] | D. | (-3,1) |
12.用秦九韶算法计算多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6,当x=-4时,v4的值为( )
| A. | -57 | B. | 220 | C. | -845 | D. | 3392 |
19.数列1×4,2×5,3×6,…,n(n+3),…则它的前n项和Sn=( )
| A. | $\frac{1}{3}$n(n+1)(n+2) | B. | $\frac{1}{3}$n(n+1)(n+3) | C. | $\frac{1}{3}$n(n+1)(n+4) | D. | $\frac{1}{3}$n(n+1)(n+5) |
9.如图所示的是“概率”知识的( )
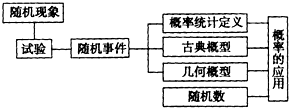

| A. | 流程图 | B. | 结构图 | C. | 程序框图 | D. | 直方图 |
16.已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-$\frac{1}{3}{x^3}$+36x+126,则使该生产厂家获取最大年利润的年产量为( )
| A. | 11万件 | B. | 9万件 | C. | 6 万件 | D. | 7万件 |
13.记cos(-80°)=k,那么tan80°=( )
| A. | $\frac{\sqrt{1-{k}^{2}}}{k}$ | B. | -$\frac{\sqrt{1-{k}^{2}}}{k}$ | C. | $\frac{k}{\sqrt{1-{k}^{2}}}$ | D. | -$\frac{k}{\sqrt{1-{k}^{2}}}$ |
14.设xi,ai(i=1,2,3)均为正实数,甲、乙两位同学由命题:“若x1+x2=1,则$\frac{{a}_{1}}{{x}_{1}}$+$\frac{{a}_{2}}{{x}_{2}}$≤($\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$)2”分别推理得出了新命题:
甲:“若x1+x2=1,则$\frac{{a}_{1}^{2}}{{x}_{1}}$+$\frac{{a}_{2}^{2}}{{x}_{2}}$≤(a1+a2)2”;
乙:“若x1+x2+x3=1,则$\frac{{a}_{1}}{{x}_{1}}$+$\frac{{a}_{2}}{{x}_{2}}$+$\frac{{a}_{3}}{{x}_{3}}$≤($\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+$\sqrt{{a}_{3}}$)2”.
他们所用的推理方法是( )
甲:“若x1+x2=1,则$\frac{{a}_{1}^{2}}{{x}_{1}}$+$\frac{{a}_{2}^{2}}{{x}_{2}}$≤(a1+a2)2”;
乙:“若x1+x2+x3=1,则$\frac{{a}_{1}}{{x}_{1}}$+$\frac{{a}_{2}}{{x}_{2}}$+$\frac{{a}_{3}}{{x}_{3}}$≤($\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+$\sqrt{{a}_{3}}$)2”.
他们所用的推理方法是( )
| A. | 甲、乙都用演绎推理 | B. | 甲、乙都用类比推理 | ||
| C. | 甲用演绎推理,乙用类比推理 | D. | 甲用归纳推理,乙用类比推理 |