题目内容
14.若不等式(-1)na<2+$\frac{(-1)^{n+1}}{n}$对于任意正整数n都成立,则实数a的取值范围是( )| A. | $[-2,\frac{3}{2})$ | B. | $(-2,\frac{3}{2}]$ | C. | [-3,2] | D. | (-3,1) |
分析 要使不等式${(-1)^n}a<2+\frac{{{{(-1)}^{n+1}}}}{n}$对于任意正整数n恒成立,讨论n为奇数和偶数,令f(n)=(-1)n•a-$\frac{(-1)^{n+1}}{n}$,
求得最大值,由最大值小于2,列出不等式求出a的范围即可.
解答 解:由不等式${(-1)^n}a<2+\frac{{{{(-1)}^{n+1}}}}{n}$得:(-1)n•a-$\frac{(-1)^{n+1}}{n}$<2,
令f(n)=(-1)n•a-$\frac{(-1)^{n+1}}{n}$,
当n取奇数时,f(n)=-a-$\frac{1}{n}$;
当n取偶数时,f(n)=a+$\frac{1}{n}$.
所以f(n)只有两个值,当-a-$\frac{1}{n}$<a+$\frac{1}{n}$时,f(n)max=a+$\frac{1}{n}$,
即a+$\frac{1}{n}$<2,得到a<$\frac{3}{2}$;
当-a-$\frac{1}{n}$≥a+$\frac{1}{n}$时,即-a-$\frac{1}{n}$<2,得a≥-2,
所以a的取值范围为-2≤a<$\frac{3}{2}$.
故选:A.
点评 本题考查学生理解函数恒成立时的条件,利用分类讨论的数学思想解决数学问题的能力.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
9.函数y=$\frac{1}{2}$x+cosx在x∈[-$\frac{π}{2}$,$\frac{π}{2}$]上的最大值为$\frac{π}{12}$+$\frac{\sqrt{3}}{2}$.
19.在等腰直角三角形ABC中,角C为直角.在∠ACB内部任意作一条射线CM,与线段AB交于点M,则AM<AC的概率( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
6.已知函数y=2cos(ωx+φ)(ω>0)在区间[0,2π]的图象如图,那么ω等于( )
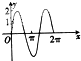

| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |