题目内容
【题目】已知椭圆
的两个焦点分别为
、
，
为椭圆
的一个短轴顶点，
．
（1）求椭圆的标准方程；
（2）若经过椭圆左焦点的直线
交椭圆于
、
两点，
为椭圆的右顶点，求
面积的最大值．
【答案】（1）
（2）
【解析】
（1）根据椭圆几何条件
，根据
可得椭圆
的标准方程．
（2）设直线
的方程与椭圆方程联立，利用根与系数的关系可得
，利用
可面积函数关系式，最后通过换元利用导数研究其单调性即可得出．
解：（1）∵椭圆
的两个焦点分别为
、
，
为椭圆的一个短轴顶点， 
．∴
，
因为
，
，
，
所以
，
，
，
∴椭圆的标准方程为：．
（2）由题意可得：直线的斜率不为
，设直线的方程为：
．
设
，
．
联立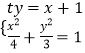
，化为：
，
，∴
，
，
∴
∴
．
令
，可得：
．
∴
，
，
单调递减，
可得
，即
时，函数取得最大值，即
，
∴
面积的最大值为．
【题目】某班数学兴趣小组对函数
的图象和性质将进行了探究，探究过程如下，请补充完整．
（1）自变量
的取值范围是除
外的全体实数，与
的几组对应值列表如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中，
_________；
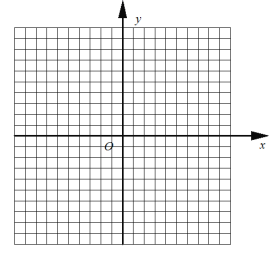
（2）根据上表数据，在如图所示的平面直角坐标系中描点并画出了函数图象的一部分，请画出该函数图象的另一部分；
（3）观察函数图象，写出一条函数性质；
（4）进一步探究函数图象发现：
①函数图象与轴交点情况是________，所以对应方程
的实数根的情况是________；
②方程
有_______个实数根；
③关于的方程
有
个实数根，
的取值范围是________．
【题目】“有黑扫黑、无黑除恶、无恶治乱”，维护社会稳定和和平发展.扫黑除恶期间，大量违法分子主动投案，某市公安机关对某月连续7天主动投案的人员进行了统计，
表示第
天主动投案的人数，得到统计表格如下：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
（1）若与具有线性相关关系，请根据上表提供的数据，用最小二乘法求出关于的线性回归方程
；
（2）判定变量与之间是正相关还是负相关.（写出正确答案，不用说明理由）
（3）预测第八天的主动投案的人数（按四舍五入取到整数）.
参考公式：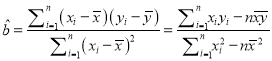
， 
.