题目内容
【题目】某班数学兴趣小组对函数![]() 的图象和性质将进行了探究,探究过程如下,请补充完整.
的图象和性质将进行了探究,探究过程如下,请补充完整.

(1)自变量![]() 的取值范围是除
的取值范围是除![]() 外的全体实数,
外的全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() _________;
_________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象,写出一条函数性质;
(4)进一步探究函数图象发现:
①函数图象与![]() 轴交点情况是________,所以对应方程
轴交点情况是________,所以对应方程![]() 的实数根的情况是________;
的实数根的情况是________;
②方程![]() 有_______个实数根;
有_______个实数根;
③关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是________.
的取值范围是________.
【答案】(1)![]() ;(2)图象见解析;(3)函数
;(2)图象见解析;(3)函数![]() 的单调递减区间为
的单调递减区间为![]() (答案不唯一);(4)①无交点,无实数根;②
(答案不唯一);(4)①无交点,无实数根;②![]() ;③
;③![]() .
.
【解析】
(1)把![]() 代入
代入![]() 求得
求得![]() 的值,即可得出
的值,即可得出![]() 的值;
的值;
(2)根据表格提供的数据描点,连线即可得到函数![]() 的另一部分图象;
的另一部分图象;
(3)观察图象,总结出函数的性质即可;
(4)①由于![]() 的值不能为
的值不能为![]() ,故函数值也不能为
,故函数值也不能为![]() ,从而可得出函数图象与
,从而可得出函数图象与![]() 轴无交点,因而
轴无交点,因而![]() 无实数根;
无实数根;
②方程![]() 的实数根的个数可以看作函数
的实数根的个数可以看作函数![]() 与直线
与直线![]() 的交点个数,画出图象即可得到结论;
的交点个数,画出图象即可得到结论;
③由②的图象即可得到结果.
(1)把![]() 代入
代入![]() 得,
得,![]() ,所以,
,所以,![]() ;
;
(2)如图所示:
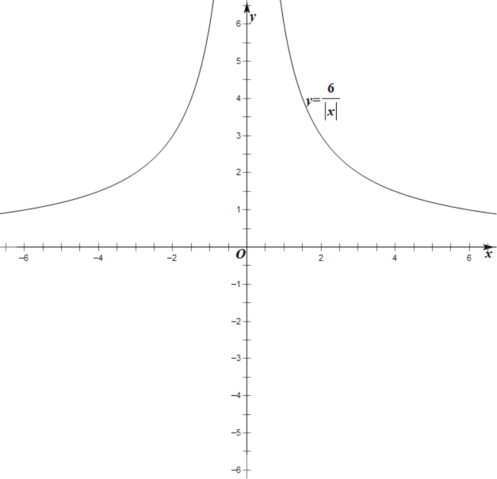
(3)观察图象可知,函数![]() 的单调递减区间为
的单调递减区间为![]() (答案不唯一);
(答案不唯一);
(4)①![]() ,
,![]() ,所以,函数
,所以,函数![]() 的图象与
的图象与![]() 轴无交点,则方程
轴无交点,则方程![]() 无实数根;
无实数根;
②求方程![]() 的根的个数,可以看成函数
的根的个数,可以看成函数![]() 与直线
与直线![]() 的交点个数,如图,
的交点个数,如图,
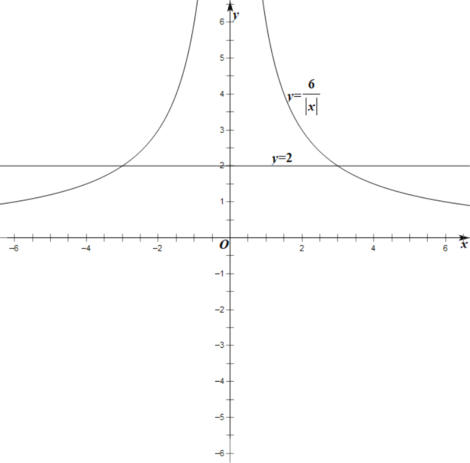
函数![]() 与直线
与直线![]() 有两个交点,故方程
有两个交点,故方程![]() 有
有![]() 个实数根,
个实数根,
③由②的图象可以得出,关于![]() 的方程
的方程![]() 有
有![]() 个实数根,
个实数根,![]() 的取值范围是
的取值范围是![]() .
.

【题目】为了整顿道路交通秩序,某地考虑对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通人中随机抽取200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如下数据:
处罚金额 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
(1)当处罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(2)将选取的200人中会闯红灯的市民分为两类:![]() 类市民在罚金不超过10元时就会改正行为;
类市民在罚金不超过10元时就会改正行为;![]() 类是其它市民.现对
类是其它市民.现对![]() 类与
类与![]() 类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为
类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为![]() 类市民的概率是多少?
类市民的概率是多少?
【题目】每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时,便会想起电影《泰坦尼克号》中一暮暮感人画面,让我们明白了什么是人类的“真、善、美”.为了推动我市旅游发展和带动全市经济,更为了向外界传递遂宁人民的“真、善、美”.我市某地将按“泰坦尼克号”原型![]() 比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市
比例重新修建.为了了解该旅游开发在大众中的熟知度,随机从本市![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该旅游开发将在我市哪个地方建成?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数 占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
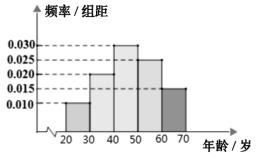
(1)求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄在
人,求所抽取的人中恰好没有年龄在![]() 段的概率.
段的概率.