题目内容
【题目】已知函数f(x)=loga(![]() )(0<a<1,b>0)为奇函数,当x∈(﹣1,a]时,函数y=f(x)的值域是(﹣∞,1].
)(0<a<1,b>0)为奇函数,当x∈(﹣1,a]时,函数y=f(x)的值域是(﹣∞,1].
(1)确定b的值;
(2)证明函数y=f(x)在定义域上单调递增,并求a的值;
(3)若对于任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)>0恒成立,求k的取值范围.
【答案】(1)b=1;(2)见解析;(3)![]()
【解析】
(1)利用f(﹣x)+f(x)=0求出b的值.(2)利用函数单调性的定义证明函数y=f(x)在定义域上单调递增,再利用y=f(x)的值域是(﹣∞,1]求出a的值.(3)首先转化为t2﹣2t>k﹣2t2,再转化为k<3t2﹣2t的最小值,求3t2﹣2t的最小值即得解.
(1)∵函数f(x)=loga(![]() )(0<a<1,b>0)为奇函数,
)(0<a<1,b>0)为奇函数,
∴f(﹣x)=﹣f(x),即f(﹣x)+f(x)=0,
∴loga![]() +loga
+loga![]() =loga(
=loga(![]()
![]() )=0,即
)=0,即![]()
![]() =1,
=1,
∴1﹣x2=b2﹣x2,即b2=1,解得b=1(﹣1舍去),
当b=1时,函数f(x)=loga![]() 为奇函数,满足条件.
为奇函数,满足条件.
(2)证明:设x1,x2∈(﹣1,1),且x1<x2,由g(x)=![]() =﹣1+
=﹣1+![]() ,
,
g(x1)﹣g(x2)=![]() ,
,
x1,x2∈(﹣1,1),且x1<x2,可得x2﹣x1>0,(1+x1)(1+x2)>0,
则g(x1)﹣g(x2)>0,即有g(x)在(﹣1,1)递减,
由f(x)=logag(x),0<a<1可得,
f(x)在(﹣1,1)递增;
∴函数f(x)=loga![]() 在x∈(﹣1,a)上单调递增,
在x∈(﹣1,a)上单调递增,
∵当x∈(﹣1,a]时,函数f(x)的值域是(﹣∞,1],
∴f(a)=1,即f(a)=loga![]() =1,∴
=1,∴![]() =a,
=a,
即1﹣a=a+a2,∴a2+2a﹣1=0,解得a=﹣1±![]() ,∵0<a<1,∴a=﹣1+
,∵0<a<1,∴a=﹣1+![]() ;
;
(3)对于任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)>0恒成立,
即有f(t2﹣2t)>﹣f(2t2﹣k)=f(k﹣2t2),
由f(x)在(﹣1,1)递增,
可得k<3t2﹣2t的最小值,
由3t2﹣2t=3(t﹣![]() )2﹣
)2﹣![]() ,可得t=
,可得t=![]() ,取得最小值﹣
,取得最小值﹣![]() ,可得k<﹣
,可得k<﹣![]() .检验成立.
.检验成立.
则k的取值范围是(﹣∞,﹣![]() ).
).

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案【题目】某班“数学兴趣小组”对函数y=﹣x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | ﹣2 |
| m | 2 | 1 | 2 | 1 |
| ﹣2 | … |
其中,m= .
(2)根据上表数据,在如图所示的平面直角坐标系中描点,画出了函数图象的一部分,请画出该函数图象的另一部分.
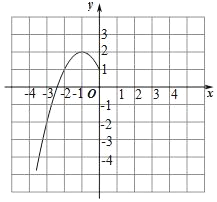
(3)观察函数图象,写出两条函数的性质./p>
(4)进一步探究函数图象发现:
①方程﹣x2+2|x|+1=0有 个实数根;
②关于x的方程﹣x2+2|x|+1=a有4个实数根时,a的取值范围是 .
【题目】为了整顿道路交通秩序,某地考虑对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通人中随机抽取200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如下数据:
处罚金额 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
(1)当处罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(2)将选取的200人中会闯红灯的市民分为两类:![]() 类市民在罚金不超过10元时就会改正行为;
类市民在罚金不超过10元时就会改正行为;![]() 类是其它市民.现对
类是其它市民.现对![]() 类与
类与![]() 类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为
类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为![]() 类市民的概率是多少?
类市民的概率是多少?



