题目内容
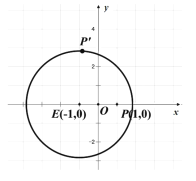
【题目】如图,一张坐标纸上一已作出圆![]() 及点
及点![]() ,折叠此纸片,使
,折叠此纸片,使![]() 与圆周上某点
与圆周上某点![]() 重合,每次折叠都会留下折痕,设折痕与直线
重合,每次折叠都会留下折痕,设折痕与直线![]() 的交点为
的交点为![]() ,令点
,令点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 与轨迹
与轨迹![]() 交于两个不同的点
交于两个不同的点![]() ,且直线
,且直线![]() 与以
与以![]() 为直径的圆相切,若
为直径的圆相切,若![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)折痕为![]() 的垂直平分线,则
的垂直平分线,则![]() ,推导出
,推导出![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,且且
为焦点的椭圆,且且![]() ,
,![]() ,由此能求出的轨迹
,由此能求出的轨迹![]() 的方程.
的方程.
(2)![]() 与以
与以![]() 为直径的圆
为直径的圆![]() 相切,,从而
相切,,从而![]() ,由
,由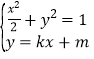 ,得
,得![]() ,由此利用根的判别式、韦达定理、向量的数量积、弦长公式、三角形面积公式,能求出
,由此利用根的判别式、韦达定理、向量的数量积、弦长公式、三角形面积公式,能求出![]() 的面积的取值范围.
的面积的取值范围.
试题解析:
(1)折痕为![]() 的垂直平分线,则
的垂直平分线,则![]() ,由题意知圆
,由题意知圆![]() 的半径为
的半径为![]() ,
,
∴![]() ,
,
∴![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆,且
为焦点的椭圆,且![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)![]() 与以
与以![]() 为直径的圆
为直径的圆![]() 相切,则
相切,则![]() 到
到![]() 即直线
即直线![]() 的距离:
的距离:
![]() ,即
,即![]() ,
,
由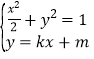 ,消去
,消去![]() ,得
,得![]() ,
,
∵直线![]() 与椭圆交于两个不同点,
与椭圆交于两个不同点,
∴![]() ,
,![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]()
![]() ,
,
又![]()
![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
![]()
![]()
![]()
设![]() ,则
,则![]() ,∴
,∴![]()
![]() ,
,![]() ,
,
∵![]() 关于
关于![]() 在
在![]() 单调递增,∴
单调递增,∴![]() ,∴
,∴![]() 的面积的取值范围是
的面积的取值范围是![]() .
.

练习册系列答案
相关题目