题目内容
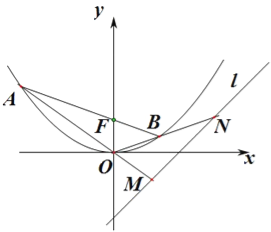
【题目】已知抛物线C的顶点为O(0,0),焦点F(0,1)
(Ⅰ)求抛物线C的方程;
(Ⅱ)过F作直线交抛物线于A、B两点.若直线OA、OB分别交直线l:y=x﹣2于M、N两点,求|MN|的最小值.
【答案】(1)x2=4y
(2)当t=﹣![]() 时,|MN|的最小值是
时,|MN|的最小值是![]()
【解析】(I)由题意可设抛物线C的方程为x2=2py(p>0)则![]() =1,解得p=2,故抛物线C的方程为x2=4y
=1,解得p=2,故抛物线C的方程为x2=4y
(II)设A(x1,y1),B(x2,y2),直线AB的方程为y=kx+1
由![]() 消去y,整理得x2﹣4kx﹣4=0
消去y,整理得x2﹣4kx﹣4=0
所以x1+x2=4k,x1x2=﹣4,从而有|x1﹣x2|=![]() =4
=4![]()
由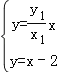 解得点M的横坐标为xM=
解得点M的横坐标为xM=![]() =
=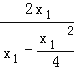 =
=![]() ,
,
同理可得点N的横坐标为xN=![]()
所以|MN|=![]() |xM﹣xN|=
|xM﹣xN|=![]() |
|![]() ﹣
﹣![]() |=8
|=8![]() |
|![]() |=
|=![]()
令4k﹣3=t,t不为0,则k=![]()
当t>0时,|MN|=2![]()
![]() >2
>2![]()
当t<0时,|MN|=2![]()
![]() =2
=2![]()
![]() ≥
≥![]()
综上所述,当t=﹣![]() 时,|MN|的最小值是
时,|MN|的最小值是![]()

练习册系列答案
相关题目
【题目】为了解高校学生平均每天使用手机的时间长短是否与性别有关,某调查小组随机抽取了25 名男生、10名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机 | 平均每天使用手机 | 合计 | |
男生 | 15 | 10 | 25 |
女生 | 3 | 7 | 10 |
合计 | 18 | 17 | 35 |
(I)在参与调查的平均每天使用手机不超过3小时的7名女生中,有4人使用国产手机,从这7名女生中任意选取2人,求至少有1人使用国产手机的概率;
(II) 根据列联表,是否有90%的把握认为学生使用手机的时间长短与性别有关(![]() 的观测值
的观测值![]() 精确到0.01).
精确到0.01).
附:
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考公式: 
![]()