��Ŀ����
����Ŀ����ѧϰ����ʱ�����Ǿ����ˡ�ȷ�������ı���ʽ���ú���ͼ���о������ʡ������ú���������⡰��ѧϰ���̣��ڻ�����ͼ��ʱ������ͨ���б�����㡢���ߵķ�����������ѧ�ĺ���ͼ��ͬʱ������Ҳѧϰ������ֵ������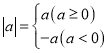 ��
��
������澭����ѧϰ���̣������������������⣺
�ں���![]() �У���
�У���![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��
��1������������ı���ʽ��
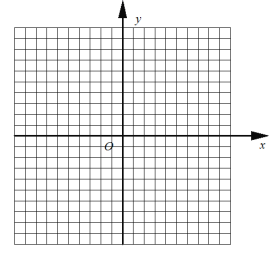
��2���ڸ�����ƽ��ֱ������ϵ�У���ֱ�ӻ����˺�����ͼ��д������������������ʣ�
��3����ͼ����������![]() ��ͼ����������ĺ���ͼ��ֱ��д������ʽ
��ͼ����������ĺ���ͼ��ֱ��д������ʽ![]() �Ľ⼯��
�Ľ⼯��
���𰸡���1��![]() ����2��ͼ�����ʼ���������3��
����2��ͼ�����ʼ���������3��![]() ��
��
��������
��1������![]() ��
��![]() ��������뺯��
��������뺯��![]() �Ľ���ʽ�����
�Ľ���ʽ�����![]() ��
��![]() ��ֵ���ɴ˿ɵó��ú����Ľ���ʽ��
��ֵ���ɴ˿ɵó��ú����Ľ���ʽ��
��2����������ݣ�1���еı���ʽ���Ի����ú�����ͼ���ͼ��ɵó��ú����ĶԳ����뵥���ԣ�
��3�����������ͼ�����ֱ��д������ʽ�Ľ⼯��
��1������![]() ��
��![]() ��������뺯��
��������뺯��![]() �Ľ���ʽ����
�Ľ���ʽ���� �����
�����![]() ,
,
���ԣ������Ľ���ʽΪ![]() ��
��
��2��ͼ�����£�

����![]() ��ͼ�����ֱ��
��ͼ�����ֱ��![]() �Գƣ��ú����ĵ����ݼ�����Ϊ
�Գƣ��ú����ĵ����ݼ�����Ϊ![]() ��������������Ϊ
��������������Ϊ![]() ����СֵΪ
����СֵΪ![]() ��
��
��3��ͼ�����£�

�۲�ͼ��ɵò���ʽ![]() �Ľ⼯Ϊ��
�Ľ⼯Ϊ��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij������ѧ��ȤС�����Ժ���y����x2+2|x|+1��ͼ������ʽ�����̽����̽���������£��벹��������
��1���Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧֵ�б����£�
x | �� | ��3 | �� | ��2 | ��1 | 0 | 1 | 2 |
| 3 | �� |
y | �� | ��2 |
| m | 2 | 1 | 2 | 1 |
| ��2 | �� |
����m��������
��2�������ϱ����ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬�����˺���ͼ���һ���֣��뻭���ú���ͼ�����һ���֣�
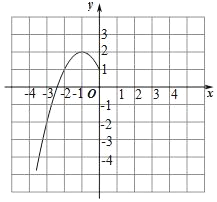
��3���۲캯��ͼ��д���������������ʣ�/p>
��4����һ��̽������ͼ���֣�
�ٷ��̩�x2+2|x|+1��0��������ʵ������
�ڹ���x�ķ��̩�x2+2|x|+1��a��4��ʵ����ʱ��a��ȡֵ��Χ��������