题目内容
已知函数f(x)= ,g(x)=
,g(x)= .
.
(1)证明f(x)满足f(-x)=-f(x),并求f(x)的单调区间;
(2)分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式,并加以证明.
 ,g(x)=
,g(x)= .
.(1)证明f(x)满足f(-x)=-f(x),并求f(x)的单调区间;
(2)分别计算f(4)-5f(2)g(2)和f(9)-5f(3)g(3)的值,由此概括出涉及函数f(x)和g(x)的对所有不等于零的实数x都成立的一个等式,并加以证明.
(1)证明见解析(2)f(x2)-5f(x)g(x)=0
(1)证明 f(-x)=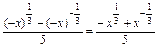 =-f(x),
=-f(x),
设x1>x2>0,由于y=x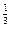 在R上递增,∴x
在R上递增,∴x >x
>x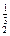 .又(x1x2)-
.又(x1x2)-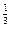 >0,
>0,
∴f(x1)-f(x2)=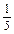 (x
(x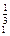 -x1
-x1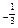 -x2
-x2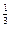 +
+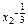 )=
)=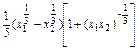 >0.
>0.
即f(x)在(0,+∞)上递增.
同理f(x)在(-∞,0)上也递增.
故f(x)在(-∞,0)和(0,+∞)上单调递增.
(2)解 f(4)-5f(2)g(2)=0,f(9)-5f(3)g(3)=0,
且f(x2)-5f(x)g(x)=0.
证明如下:
f(x2)-5f(x)g(x)=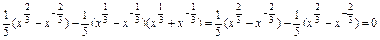
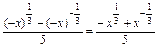 =-f(x),
=-f(x),设x1>x2>0,由于y=x
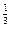 在R上递增,∴x
在R上递增,∴x >x
>x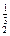 .又(x1x2)-
.又(x1x2)-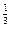 >0,
>0,∴f(x1)-f(x2)=
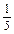 (x
(x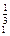 -x1
-x1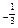 -x2
-x2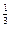 +
+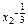 )=
)=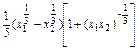 >0.
>0.即f(x)在(0,+∞)上递增.
同理f(x)在(-∞,0)上也递增.
故f(x)在(-∞,0)和(0,+∞)上单调递增.
(2)解 f(4)-5f(2)g(2)=0,f(9)-5f(3)g(3)=0,
且f(x2)-5f(x)g(x)=0.
证明如下:
f(x2)-5f(x)g(x)=
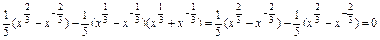

练习册系列答案
相关题目
 。
。 ;
; 。
。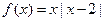 (1)画出函数的图像,写出
(1)画出函数的图像,写出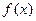 的单调区间;
的单调区间;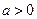 ,求
,求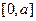 上的最大值
上的最大值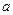
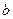
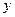 (元)表示为里程
(元)表示为里程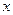 (km)的函数
(km)的函数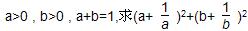 的最小值。
的最小值。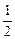 ],都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0.
],都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0. 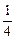 );
);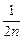 ),求
),求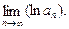
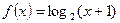 ,当点
,当点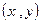 在函数
在函数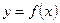 的图象上时,点
的图象上时,点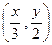 在函数
在函数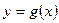 的图象上。
的图象上。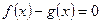 方程的根
方程的根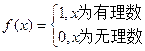 ,
,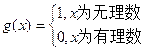 ,则
,则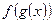 =_____________。
=_____________。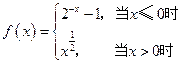 若
若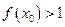 ,求
,求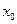 的取值范围 .
的取值范围 .