题目内容
已知抛物线C的参数方程为
(t为参数),若斜率为1的直线经过抛物线C的焦点,且与圆(x-4)2+y2=r2(r>0)相切,则r=______.
|
∵抛物线C的参数方程为
则抛物线的标准方程为:y2=8x
则抛物线C的焦点的坐标为(2,0)
又∵斜率为1的直线经过抛物线C的焦点
则直线的方程为y=x-2,即经x-y-2=0
由直线与圆(x-4)2+y2=r2,则
r=
=
故答案为:
|
则抛物线的标准方程为:y2=8x
则抛物线C的焦点的坐标为(2,0)
又∵斜率为1的直线经过抛物线C的焦点
则直线的方程为y=x-2,即经x-y-2=0
由直线与圆(x-4)2+y2=r2,则
r=
| 4-2 | ||
|
| 2 |
故答案为:
| 2 |

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
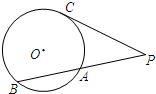
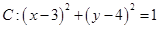 和两点
和两点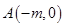 ,
,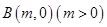 ,若圆
,若圆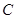 上存在点
上存在点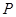 ,使得
,使得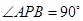 ,则
,则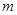 的最大值为( )
的最大值为( )
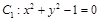 和
和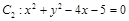 的位置关系是( )
的位置关系是( )