题目内容
若直线l:4x+3y+a=0和圆C:x2+y2+2x-4y+1=0有公共点,则实数a的取值范围是( )
| A.[-12,8] | B.[-8,12] | C.[-22,18] | D.[-18,22] |
∵圆C:x2+y2+2x-4y+1=0,
∴(x+1)2+(y-2)2=4,圆心为C(-1,2),半径为2.
∵直线l:4x+3y+a=0和圆C:x2+y2+2x-4y+1=0有公共点,
∴圆心C到直线l的距离d=
=
≤2,
∴-12≤a≤8.
故选A.
∴(x+1)2+(y-2)2=4,圆心为C(-1,2),半径为2.
∵直线l:4x+3y+a=0和圆C:x2+y2+2x-4y+1=0有公共点,
∴圆心C到直线l的距离d=
| |-4+6+a| |
| 5 |
| |a+2| |
| 5 |
∴-12≤a≤8.
故选A.

练习册系列答案
相关题目
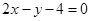 上,若圆M上不存在点N,使
上,若圆M上不存在点N,使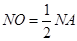 ,其中A(0,3),则圆心M横坐标的取值范围 .
,其中A(0,3),则圆心M横坐标的取值范围 .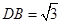 ,则DC= .
,则DC= .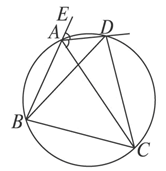
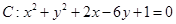 ,直线
,直线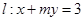 .
. 与
与 相切,求
相切,求 的值;
的值;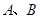 两点,且
两点,且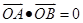 (其中
(其中 为坐标原点),若存在,求出
为坐标原点),若存在,求出