题目内容
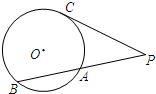
如图,PAB、PC分别是圆O的割线和切线(C为切点),若PA=AB=3,则PC的长为( )
A.6
| B.6 | C.3
| D.3 |

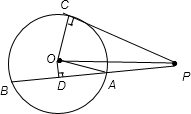
由题意可得:设圆的圆心为O,半径为r,所以OC=OA=r.
由圆的性质可得:PC2=OP2-r2,
又因为PA=AB=3,所以AD=1.5.
所以OD2+1.52=r2…①
OD2+4.52=OP2…②
所以②-①可得:OP2-r2=4.52-1.52=18,
所以PC=3
.
故选C.
由圆的性质可得:PC2=OP2-r2,
又因为PA=AB=3,所以AD=1.5.
所以OD2+1.52=r2…①
OD2+4.52=OP2…②
所以②-①可得:OP2-r2=4.52-1.52=18,
所以PC=3
| 2 |
故选C.


练习册系列答案
相关题目
 与圆
与圆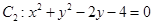 相交于A、B两点.
相交于A、B两点. 上的圆的方程.
上的圆的方程.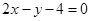 上,若圆M上不存在点N,使
上,若圆M上不存在点N,使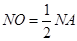 ,其中A(0,3),则圆心M横坐标的取值范围 .
,其中A(0,3),则圆心M横坐标的取值范围 .