题目内容
在直三棱柱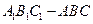 中,
中,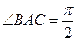 ,
,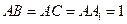 . 已知G与E分别为
. 已知G与E分别为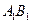 和
和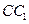 的中点,D与F分别为线段
的中点,D与F分别为线段 和
和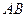 上的动点(不包括端点). 若
上的动点(不包括端点). 若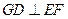 ,则线段
,则线段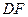 的长度的取值范围为
的长度的取值范围为
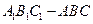 中,
中,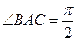 ,
,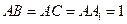 . 已知G与E分别为
. 已知G与E分别为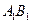 和
和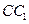 的中点,D与F分别为线段
的中点,D与F分别为线段 和
和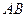 上的动点(不包括端点). 若
上的动点(不包括端点). 若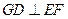 ,则线段
,则线段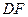 的长度的取值范围为
的长度的取值范围为A.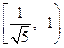 | B. | C. | D. |
A
建立直角坐标系,以A为坐标原点,AB为x轴,AC为y轴,AA1为z轴,则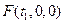 (
(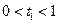 ),
),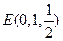 ,
,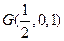 ,
,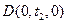 (
(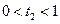 )。所以
)。所以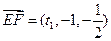 ,
,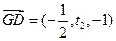 。因为
。因为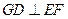 ,所以
,所以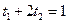 ,由此推出
,由此推出 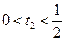 。又
。又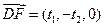 ,
,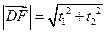
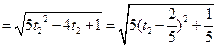 ,从而有
,从而有 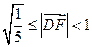 。
。
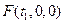 (
(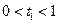 ),
),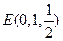 ,
,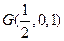 ,
,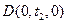 (
(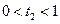 )。所以
)。所以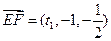 ,
,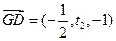 。因为
。因为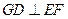 ,所以
,所以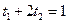 ,由此推出
,由此推出 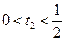 。又
。又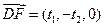 ,
,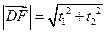
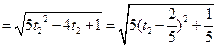 ,从而有
,从而有 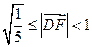 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
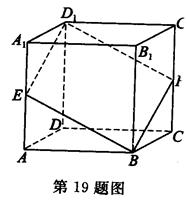
 中,底面
中,底面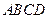 是矩形,
是矩形,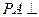 平面
平面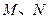 分别是
分别是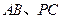 的中点,
的中点,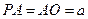 .
.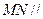 平面
平面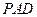 ;
;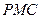 ⊥平面
⊥平面 .
.
 ,底面
,底面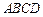 为矩形,侧棱
为矩形,侧棱 ,其中
,其中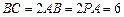 ,
,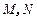 为侧棱
为侧棱 上的两个三等分点,如图所示.
上的两个三等分点,如图所示.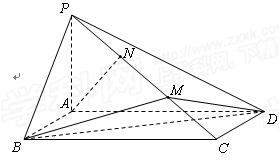
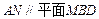 ;
;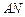 与
与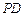 所成角的余弦值;
所成角的余弦值;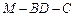 的余弦值.
的余弦值.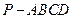 中,底面ABCD是菱形,
中,底面ABCD是菱形,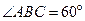 ,
,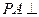 平面ABCD,点M,N分别为BC,PA的中
平面ABCD,点M,N分别为BC,PA的中 点,且
点,且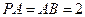
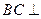 平面AMN;
平面AMN; 的体积;
的体积; 使得
使得 平面ACE;若存在,求出PE的长,若不存在,说明理由。
平面ACE;若存在,求出PE的长,若不存在,说明理由。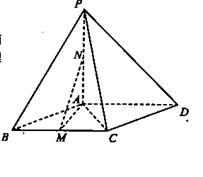
 ,在四边形ABCD中,∠ADC=∠DAB=90
,在四边形ABCD中,∠ADC=∠DAB=90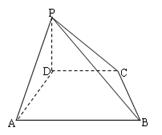
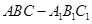 中,侧棱
中,侧棱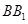 与底面成
与底面成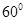 角,
角,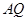 ⊥底面
⊥底面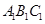 于
于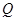 ,
, 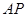 ⊥侧面
⊥侧面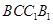 于
于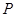 ,且
,且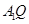 ⊥
⊥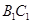 ,
,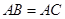 ,
,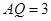 ,
,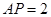 则顶点
则顶点 到棱
到棱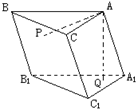
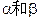 为平面,
为平面,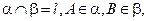 AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角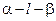 的大小为
的大小为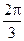 ,求:
,求: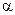 的距离;
的距离;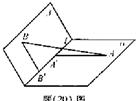
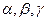 是三个不重合的平面,
是三个不重合的平面,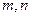 是不重合的直线,给出下列命题:
是不重合的直线,给出下列命题: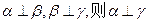 ;②若
;②若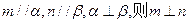 ;③若
;③若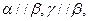 则
则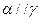 ;④若
;④若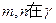 内的射影互相垂直,则
内的射影互相垂直,则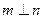 ,其中错误命题有 ( )
,其中错误命题有 ( )