题目内容
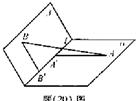
(本小题满分12分)如图,在棱长为1的正方体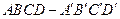 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥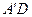 ,截面PQGH∥
,截面PQGH∥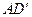 .
.
(Ⅰ)证明:平面PQEF和平面PQGH互相垂直;
(Ⅱ)证明:截面PQEF和截面PQGH面积之和是定值,
并求出这个值;
(Ⅲ)若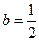 ,求
,求 与平面PQEF所成角的正弦值.
与平面PQEF所成角的正弦值.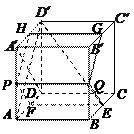
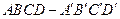 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥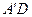 ,截面PQGH∥
,截面PQGH∥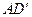 .
.(Ⅰ)证明:平面PQEF和平面PQGH互相垂直;
(Ⅱ)证明:截面PQEF和截面PQGH面积之和是定值,
并求出这个值;
(Ⅲ)若
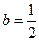 ,求
,求 与平面PQEF所成角的正弦值.
与平面PQEF所成角的正弦值.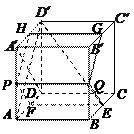
(Ⅰ)同解析(Ⅱ)截面PQEF和截面PQGH面积之和为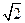 ,是定值.(Ⅲ)
,是定值.(Ⅲ)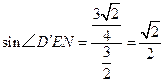 .
.
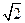 ,是定值.(Ⅲ)
,是定值.(Ⅲ)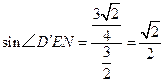 .
.解法一:
(Ⅰ)证明:在正方体中,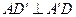 ,
,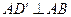 ,
,
又由已知可得
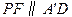 ,
,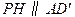 ,
,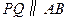 ,
,
所以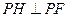 ,
,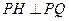 ,
,
所以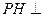 平面
平面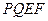 .
.
所以平面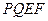 和平面
和平面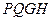 互相垂直. 4分
互相垂直. 4分
(Ⅱ)证明:由(Ⅰ)知
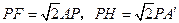 ,又截面PQEF和截面PQGH都是矩形,且PQ=1,所以截面PQEF和截面PQGH面积之和是
,又截面PQEF和截面PQGH都是矩形,且PQ=1,所以截面PQEF和截面PQGH面积之和是
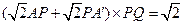 ,是定值. 8分
,是定值. 8分
(Ⅲ)解:设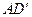 交
交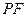 于点
于点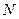 ,连结
,连结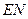 ,
,
因为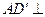 平面
平面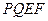 ,
,
所以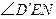 为
为 与平面
与平面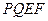 所成的角.
所成的角.
因为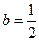 ,所以
,所以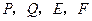 分别为
分别为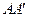 ,
, ,
, ,
,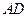 的中点.
的中点.
可知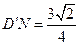 ,
,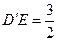 .
.
所以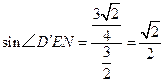 . 12分
. 12分
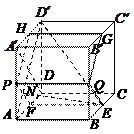
解法二:
以D为原点,射线DA,DC,DD′分别为x,y,z轴的正半轴建立如图的空间直角坐标系D-xyz.由已知得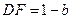 ,故
,故
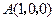 ,
,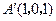 ,
,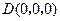 ,
,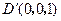 ,
,
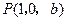 ,
,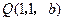 ,
,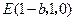 ,
,
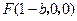 ,
,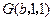 ,
,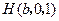 .
.
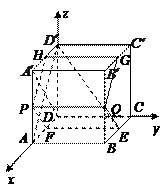
(Ⅰ)证明:在所建立的坐标系中,可得
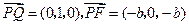 ,
,
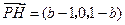 ,
,
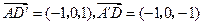 .
.
因为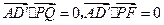 ,所以
,所以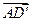 是平面PQEF的法向量.
是平面PQEF的法向量.
因为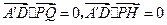 ,所以
,所以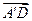 是平面PQGH的法向量.
是平面PQGH的法向量.
因为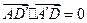 ,所以
,所以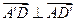 ,
,
所以平面PQEF和平面PQGH互相垂直. 4分
(Ⅱ)证明:因为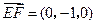 ,所以
,所以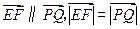 ,又
,又 ,所以PQEF为矩形,同理PQGH为矩形.
,所以PQEF为矩形,同理PQGH为矩形.
在所建立的坐标系中可求得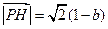 ,
, ,
,
所以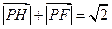 ,又
,又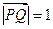 ,
,
所以截面PQEF和截面PQGH面积之和为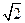 ,是定值. 8分
,是定值. 8分
(Ⅲ)解:由(Ⅰ)知 是平面
是平面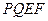 的法向量.
的法向量.
由 为
为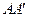 中点可知,
中点可知,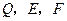 分别为
分别为 ,
, ,
,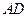 的中点.
的中点.
所以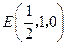 ,
, ,因此
,因此 与平面
与平面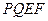 所成角的正弦值等于
所成角的正弦值等于
 . 12分
. 12分
(Ⅰ)证明:在正方体中,
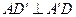 ,
,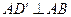 ,
,又由已知可得
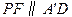 ,
,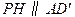 ,
,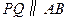 ,
,所以
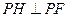 ,
,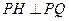 ,
,所以
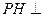 平面
平面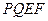 .
.所以平面
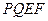 和平面
和平面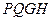 互相垂直. 4分
互相垂直. 4分(Ⅱ)证明:由(Ⅰ)知
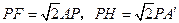 ,又截面PQEF和截面PQGH都是矩形,且PQ=1,所以截面PQEF和截面PQGH面积之和是
,又截面PQEF和截面PQGH都是矩形,且PQ=1,所以截面PQEF和截面PQGH面积之和是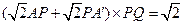 ,是定值. 8分
,是定值. 8分(Ⅲ)解:设
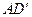 交
交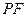 于点
于点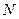 ,连结
,连结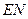 ,
,因为
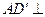 平面
平面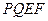 ,
,所以
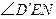 为
为 与平面
与平面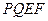 所成的角.
所成的角.因为
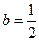 ,所以
,所以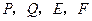 分别为
分别为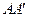 ,
, ,
, ,
,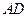 的中点.
的中点.可知
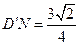 ,
,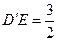 .
.所以
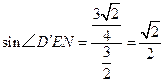 . 12分
. 12分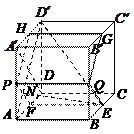
解法二:
以D为原点,射线DA,DC,DD′分别为x,y,z轴的正半轴建立如图的空间直角坐标系D-xyz.由已知得
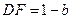 ,故
,故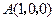 ,
,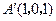 ,
,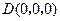 ,
,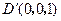 ,
,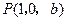 ,
,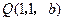 ,
,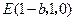 ,
,
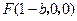 ,
,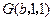 ,
,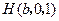 .
.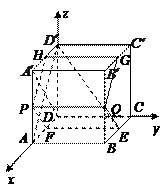
(Ⅰ)证明:在所建立的坐标系中,可得
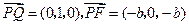 ,
,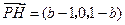 ,
,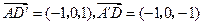 .
.因为
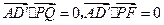 ,所以
,所以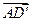 是平面PQEF的法向量.
是平面PQEF的法向量.因为
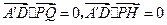 ,所以
,所以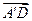 是平面PQGH的法向量.
是平面PQGH的法向量.因为
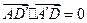 ,所以
,所以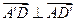 ,
,所以平面PQEF和平面PQGH互相垂直. 4分
(Ⅱ)证明:因为
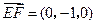 ,所以
,所以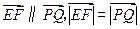 ,又
,又 ,所以PQEF为矩形,同理PQGH为矩形.
,所以PQEF为矩形,同理PQGH为矩形.在所建立的坐标系中可求得
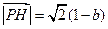 ,
, ,
,所以
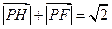 ,又
,又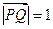 ,
,所以截面PQEF和截面PQGH面积之和为
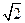 ,是定值. 8分
,是定值. 8分(Ⅲ)解:由(Ⅰ)知
 是平面
是平面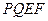 的法向量.
的法向量.由
 为
为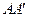 中点可知,
中点可知,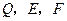 分别为
分别为 ,
, ,
,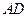 的中点.
的中点.所以
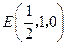 ,
, ,因此
,因此 与平面
与平面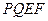 所成角的正弦值等于
所成角的正弦值等于 . 12分
. 12分
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
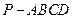 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.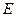 是侧棱
是侧棱 上的动点.
上的动点.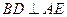
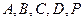 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
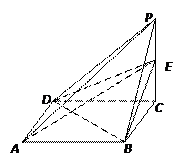
 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中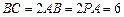 ,
,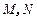 为侧棱
为侧棱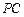 上的两个三等分点,如图所示.
上的两个三等分点,如图所示.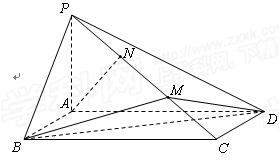
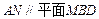 ;
;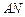 与
与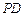 所成角的余弦值;
所成角的余弦值;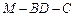 的余弦值.
的余弦值. )
)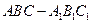 的底面边长是
的底面边长是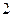 ,
, 、E是
、E是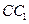 、BC的中点,AE=DE
、BC的中点,AE=DE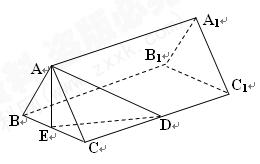
 中,
中,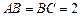 ,过
,过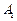 、
、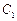 、
、 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体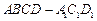 ,且这个几何体的体积为
,且这个几何体的体积为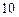 .
.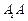 的长;
的长;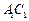 的中点为
的中点为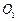 ,求异面直线
,求异面直线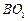 与
与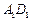 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).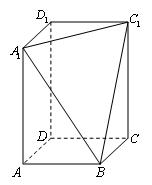
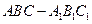 中,底面边长为
中,底面边长为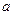 ,侧棱长为
,侧棱长为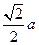 ,
,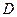 是棱
是棱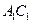 的中点.
的中点.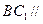 平面
平面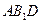 ;(Ⅱ)求二面角
;(Ⅱ)求二面角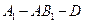 的大小;
的大小;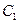 到平面
到平面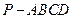 中,底面ABCD是菱形,
中,底面ABCD是菱形,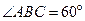 ,
,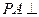 平面ABCD,点M,N分别为BC,PA的中
平面ABCD,点M,N分别为BC,PA的中 点,且
点,且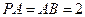
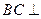 平面AMN;
平面AMN;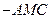 的体积;
的体积; 使得
使得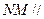 平面ACE;若存在,求出PE的长,若不存在,说明理由。
平面ACE;若存在,求出PE的长,若不存在,说明理由。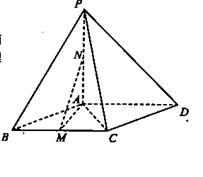
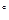 ,在四边形ABCD中,∠ADC=∠DAB=90
,在四边形ABCD中,∠ADC=∠DAB=90
 为平面,
为平面,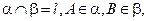 AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角
AB=5,A,B在棱l上的射影分别为A′,B′,AA′=3,BB′=2.若二面角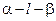 的大小为
的大小为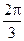 ,求:
,求: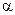 的距离;
的距离;