题目内容
(本大题满分12分)如图,P是边长为1的正六边形ABCDEF所在平面外一点,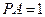 ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。
(Ⅰ)证明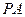 ⊥
⊥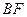 ;
;
(Ⅱ)求面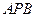 与面
与面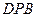 所成二面角的大小。
所成二面角的大小。
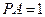 ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。(Ⅰ)证明
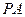 ⊥
⊥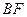 ;
;(Ⅱ)求面
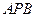 与面
与面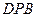 所成二面角的大小。
所成二面角的大小。
同解析
(Ⅰ)在正六边形ABCDEF中, 为等腰三角形,
为等腰三角形,
∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;
∵O为BF中点,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)∵PO⊥平面ABF,∴平面PBF⊥平面ABC;而O为BF中点,ABCDEF是正六边形 ,
∴A、O、D共线,且直线AD⊥BF,则AD⊥平面PBF;
又∵正六边形ABCDEF的边长为1,
∴ ,
,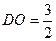 ,
,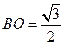 。
。
过O在平面POB内作OH⊥PB于H,连AH、DH,则AH⊥PB,DH⊥PB,
所以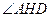 为所求二面角平面角。
为所求二面角平面角。
在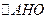 中,OH=
中,OH=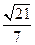 ,
, =
= 。
。
在 中,
中,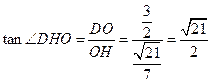 ;
;
而
 为等腰三角形,
为等腰三角形,∵P在平面ABC内的射影为O,∴PO⊥平面ABF,∴AO为PA在平面ABF内的射影;
∵O为BF中点,∴AO⊥BF,∴PA⊥BF。
(Ⅱ)∵PO⊥平面ABF,∴平面PBF⊥平面ABC;而O为BF中点,ABCDEF是正六边形 ,
∴A、O、D共线,且直线AD⊥BF,则AD⊥平面PBF;
又∵正六边形ABCDEF的边长为1,
∴
 ,
,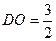 ,
,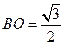 。
。过O在平面POB内作OH⊥PB于H,连AH、DH,则AH⊥PB,DH⊥PB,
所以
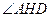 为所求二面角平面角。
为所求二面角平面角。在
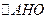 中,OH=
中,OH=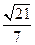 ,
, =
= 。
。在
 中,
中,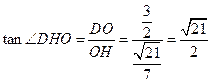 ;
;而


练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
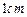 的正方体。
的正方体。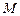 、
、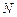 、
、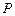 、
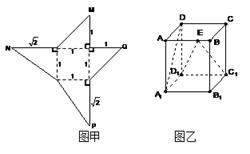
、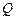 重合,则可以围成怎样的几何体?请求出此几何体的体积;
重合,则可以围成怎样的几何体?请求出此几何体的体积; 体?请按图乙中所标字母写出这几个几何体的名称;
体?请按图乙中所标字母写出这几个几何体的名称;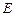 为棱
为棱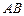 上的动点,试判断
上的动点,试判断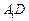 与平面
与平面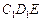 是否垂直,并说明理由。
是否垂直,并说明理由。
 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中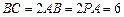 ,
, 为侧棱
为侧棱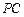 上的两个三等分点,如图所示.
上的两个三等分点,如图所示.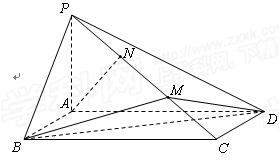
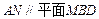 ;
;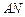 与
与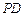 所成角的余弦值;
所成角的余弦值;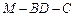 的余弦值.
的余弦值.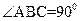 ,
,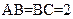 ,二面角P-AB-C为
,二面角P-AB-C为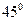 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.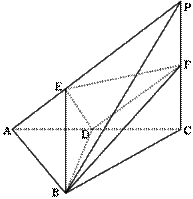
 )
)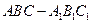 的底面边长是
的底面边长是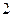 ,
, 、E是
、E是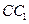 、BC的中点,AE=DE
、BC的中点,AE=DE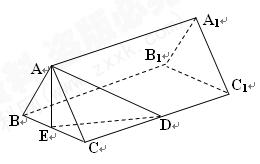
 中,
中,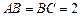 ,过
,过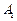 、
、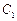 、
、 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体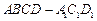 ,且这个几何体的体积为
,且这个几何体的体积为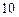 .
.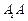 的长;
的长;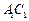 的中点为
的中点为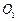 ,求异面直线
,求异面直线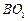 与
与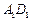 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).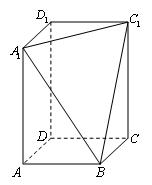
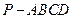 中,底面ABCD是菱形,
中,底面ABCD是菱形,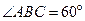 ,
,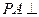 平面ABCD,点M,N分别为BC,PA的中
平面ABCD,点M,N分别为BC,PA的中 点,且
点,且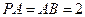
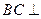 平面AMN;
平面AMN;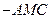 的体积;
的体积; 使得
使得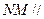 平面ACE;若存在,求出PE的长,若不存在,说明理由。
平面ACE;若存在,求出PE的长,若不存在,说明理由。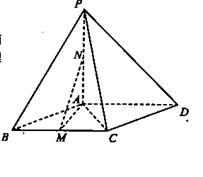
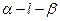 的大小为
的大小为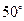 ,
,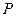 为空间中任意一点,则过点
为空间中任意一点,则过点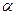 和平面
和平面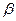 所成的角都是
所成的角都是 的直线的条数为( )
的直线的条数为( )
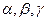 是三个不重合的平面,
是三个不重合的平面,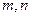 是不重合的直线,给出下列命题:
是不重合的直线,给出下列命题: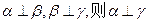 ;②若
;②若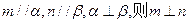 ;③若
;③若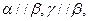 则
则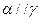 ;④若
;④若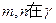 内的射影互相垂直,则
内的射影互相垂直,则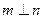 ,其中错误命题有 ( )
,其中错误命题有 ( )