题目内容
20.已知函数f(x)是R上的增函数,A(0,-2),B(3,2)是其图象上的两点,记不等式|f(x+2)|<2的解集M,则∁RM=( )| A. | (-2,1) | B. | (-1,2) | C. | (-∞,-2]∪[1,+∞) | D. | (-∞,-1]∪[2,+∞) |
分析 根据已知f(0)=-2,f(3)=2,从而由|f(x+2)|<2便得f(0)<f(x+2)<f(3),根据f(x)为增函数便得0<x+2<3,这样便可得到M,求补集即可得出∁RM.
解答 解:由条件,f(0)=-2,f(3)=2;
由|f(x+2)|<2得-2<f(x+2)<2;
∴f(0)<f(x+2)<f(3);
∵f(x)是R上的增函数;
∴0<x+2<3;
∴-2<x<1;
即M=(-2,1);
∴∁RM=(-∞,-2]∪[1,+∞).
故选C.
点评 考查函数图象上的点的坐标和函数解析式的对应关系,解绝对值不等式,以及增函数定义的运用,补集的运算.

练习册系列答案
相关题目
19.若集合A={x|1<x≤$\sqrt{3}$},B={x|0<x≤1},则A∪B=( )
| A. | {x|x>0} | B. | {x|x≤$\sqrt{3}$} | C. | {x|0≤x≤$\sqrt{3}$} | D. | {x|0<x≤$\sqrt{3}$} |
5.在下列各图中,图中两个变量具有相关关系的图是( )
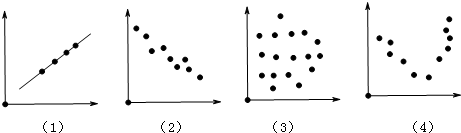

| A. | (1)(2) | B. | (1)(4) | C. | (2)(4) | D. | (2)(3) |
10.cos17°sin43°+sin17°cos43°( )
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |