题目内容
6.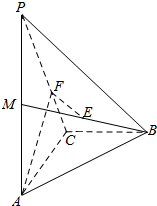 如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.
如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.(Ⅰ)求证:BC⊥AF
(Ⅱ)求$\frac{CF}{CP}$;
(Ⅲ)若异面直线EF与CA所成角为45°,求EF与面PAB所成角θ的正弦值.
分析 (Ⅰ)PA⊥面ACB,从而得到BC⊥PA,再由BC⊥AC及线面垂直判定定理即可得出BC⊥AF;
(Ⅱ)首先根据已知条件,以A为原点,AC的垂线为x轴,AC为y轴建立空间直角坐标系,求出一些点的坐标,可设$\frac{CF}{CP}=λ$,B(m,2,0),可表示出F点的坐标,而$\overrightarrow{AP}=(0,0,4)$为平面ACB的一个法向量,由EF∥面ACB,即可得到$\overrightarrow{EF}•\overrightarrow{AP}=0$,这样即可求出λ;
(Ⅲ)写出向量$\overrightarrow{EF},\overrightarrow{CA}$的坐标,根据异面直线EF与CA所成角为45°即可求出m,从而求出B点坐标,过C作CD⊥AB,则可说明$\overrightarrow{CD}$为平面PAB的法向量,并设$\overrightarrow{CD}=(x,y,0)$,根据$\overrightarrow{CD}⊥\overrightarrow{AB}$即可求出$\overrightarrow{CD}$,从而由sinθ=|cos$<\overrightarrow{EF},\overrightarrow{CD}>$|即可求得EF与面PAB所成角θ的正弦值.
解答 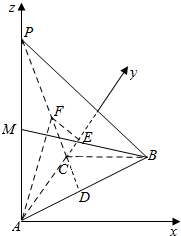 解:(Ⅰ)证明:PA⊥面ACB,BC?面ACB;
解:(Ⅰ)证明:PA⊥面ACB,BC?面ACB;
∴PA⊥BC,即BC⊥PA;
又BC⊥AC,PA∩AC=A;
∴BC⊥面PAC,AF?面PAC;
∴BC⊥AF;
(Ⅱ)如图以A为原点,AC的垂线,AC,AP三直线分别为x,y,z轴,建立空间直角坐标系,则:
A(0,0,0),C(0,2,0),P(0,0,4),M(0,0,2);
设$\frac{CF}{CP}=λ$,(0≤λ≤1),B(m,2,0),(m>0),可得$E(\frac{m}{2},1,1)$,F(0,2-2λ,4λ),则$\overrightarrow{EF}=(-\frac{m}{2},1-2λ,4λ-1)$;
因为$\overrightarrow{AP}=(0,0,4)$是平面ACB的一个法向量,EF∥面ACB;
∴$\overrightarrow{EF}⊥\overrightarrow{AP}$;
∴$\overrightarrow{EF}•\overrightarrow{AP}=4(4λ-1)=0$;
∴$λ=\frac{1}{4}$;
∴$\frac{CF}{CP}=\frac{1}{4}$;
(Ⅲ)由(Ⅱ)知$\overrightarrow{EF}=(-\frac{m}{2},\frac{1}{2},0),\overrightarrow{CA}=(0,-2,0)$;
∴$cos45°=|cos<\overrightarrow{EF},\overrightarrow{CA}>|$=$\frac{|\overrightarrow{EF}•\overrightarrow{CA}|}{|\overrightarrow{EF}||\overrightarrow{CA}|}$=$\frac{1}{\sqrt{\frac{{m}^{2}}{4}+\frac{1}{4}}•2}=\frac{\sqrt{2}}{2}$;
解得m=1;
由此$\overrightarrow{EF}=(-\frac{1}{2},\frac{1}{2},0)$,B(1,2,0);
过C作CD⊥AB,垂足为D;
又∵PA⊥面ACB,CD?面ACB;
∴CD⊥PA,PA∩AB=A;
∴CD⊥面PAB;
∴$\overrightarrow{CD}$为面PAB的法向量,设$\overrightarrow{CD}=(x,y,0)$,则:
$\overrightarrow{CD}•\overrightarrow{AB}=x+2y=0$,取y=1,则$\overrightarrow{CD}=(-2,1,0)$;
∴EF与面PAB所成角θ的正弦值:sinθ=|cos$<\overrightarrow{CD},\overrightarrow{EF}>$|=$\frac{\frac{3}{2}}{\sqrt{\frac{1}{2}}•\sqrt{5}}=\frac{3\sqrt{10}}{10}$.
点评 考查线面垂直的性质,线面垂直的判定定理,建立空间直角坐标系,利用空间向量解决线面平行、线线角,以及线面角等问题的方法,能确定空间点的坐标,向量夹角余弦的坐标公式,弄清直线和平面所成角与直线方向向量和平面法向量夹角的关系.

 阅读快车系列答案
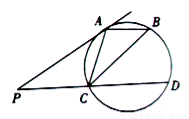
阅读快车系列答案 与圆切于点
与圆切于点 ,过
,过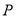 作直线与圆交于
作直线与圆交于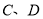 两点,点
两点,点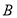 在圆上,且
在圆上,且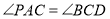 .
.
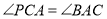 ;
;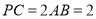 ,求
,求 .
.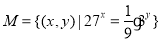 ,则下列说法正确的是( )
,则下列说法正确的是( )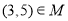 B.
B.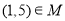
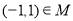 D.
D.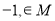

 如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,若AB=2PC=$\sqrt{2}$,D是PC的中点
如图,在三棱锥P-ABC中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,若AB=2PC=$\sqrt{2}$,D是PC的中点