题目内容
1.已知椭圆E的中心在坐标原点O,其焦点与双曲线C:${x^2}-\frac{y^2}{2}=1$的焦点重合,且椭圆E的短轴的两个端点与其一个焦点构成正三角形.(Ⅰ)求椭圆E的方程;
(Ⅱ)过双曲线C的右顶点A作直线l与椭圆E交于不同的两点P、Q.
①设M(m,0),当$\overrightarrow{MP}•\overrightarrow{MQ}$为定值时,求m的值;
②设点N是椭圆E上的一点,满足ON∥PQ,记△NAP的面积为S1,△OAQ的面积为S2,求S1+S2的取值范围.
分析 (Ⅰ)设方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,确定c,利用椭圆E的短轴的两个端点与其一个焦点构成正三角形,可得a=2b,利用a2=b2+c2,求出a,b,即可求椭圆E的方程;
(Ⅱ)①分类讨论,设l的方程为y=k(x-1),代入椭圆方程,利用韦达定理,结合向量的数量积公式,可得结论;②确定S1+S2=S△OPQ,求出|PQ|,可得面积,换元确定面积的范围即可求S1+S2的取值范围.
解答 解:(Ⅰ)由题意椭圆的焦点在x轴上,设方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,其左右焦点为F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),∴c=$\sqrt{3}$,
∵椭圆E的短轴的两个端点与其一个焦点构成正三角形,
∴a=2b,
∵a2=b2+c2,
∴a=2,b=1,
∴椭圆E的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)①双曲线C右顶点为A(1,0),
当直线l的斜率存在时,设l的方程为y=k(x-1),
代入椭圆方程得(4k2+1)x2-8k2x+4k2-4=0,
设直线l与椭圆E交点P(x1,y1),Q(x2,y2),
则x1+x2=$\frac{8{k}^{2}}{4{k}^{2}+1}$,x1x2=$\frac{4{k}^{2}-4}{4{k}^{2}+1}$,
∴$\overrightarrow{PM}$•$\overrightarrow{QM}$=m2-m(x1+x2)+x1x2+y1y2=
=$\frac{1}{4}$(4m2-8m+1)+$\frac{2m-\frac{17}{4}}{4{k}^{2}+1}$,
当2m-$\frac{17}{4}$=0,即m=$\frac{17}{8}$时,$\overrightarrow{PM}$•$\overrightarrow{QM}$=$\frac{33}{64}$.
当直线l的斜率不存在时,直线l的方程为x=1,代入椭圆方程可得x=1,y=±$\frac{\sqrt{3}}{2}$.
不妨设P(1,$\frac{\sqrt{3}}{2}$),Q(1,-$\frac{\sqrt{3}}{2}$),
由M($\frac{17}{8}$,0)可得$\overrightarrow{PM}$=($\frac{9}{8}$,-$\frac{\sqrt{3}}{2}$),$\overrightarrow{QM}$=($\frac{9}{8}$,$\frac{\sqrt{3}}{2}$),
∴$\overrightarrow{PM}$•$\overrightarrow{QM}$=$\frac{33}{64}$,
综上所述,m=$\frac{17}{8}$时,$\overrightarrow{PM}$•$\overrightarrow{QM}$为定值$\frac{33}{64}$;
②∵ON∥PQ,
∴S△NAP=S△OAP,
∴S1+S2=S△OPQ,
∵|PQ|=4$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{3{k}^{2}+1}}{4{k}^{2}+1}$,
∵原点O到直线PQ的距离为d=$\frac{|k|}{\sqrt{1+{k}^{2}}}$(k≠0),
∴S△OPQ=$\frac{1}{2}|PQ|d$=$\sqrt{\frac{4{k}^{2}(3{k}^{2}+1)}{(4{k}^{2}+1)^{2}}}$
令t=4k2+1,则k2=$\frac{t-1}{4}$(t>1),
∴S=$\frac{1}{2}$$\sqrt{\frac{3{t}^{2}-2t-1}{{t}^{2}}}$=$\frac{1}{2}$$\sqrt{-(\frac{1}{t}+1)^{2}+4}$,
∵t>1,
∴0<$\frac{1}{t}$<1,
∴0<-$(\frac{1}{t}+1)^{2}$+4<3,
∴0<S<$\frac{\sqrt{3}}{2}$.
当直线l的斜率不存在时,S△OPQ=$\frac{1}{2}×1×\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
综上所述,S1+S2的取值范围是(0,$\frac{\sqrt{3}}{2}$].
点评 本题考查椭圆方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查韦达定理,有难度.

| x | 1 | 2 | 3 | 4 |
| y | 20 | 30 | 50 | 60 |
(Ⅱ)若用$\frac{y_i}{{{x_i}+3}}$(i=1,2,3,4)表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间[0,2)内,则强化训练有效,请问这个班的强化训练是否有效?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\bar x)({y_i}-\bar y)}}}{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}$,$\hat a=\bar y-\hat b\bar x$.
样本数据x1,x2,…,xn的标准差为:s=$\sqrt{\frac{{\sum_{i=1}^n{{{({x_i}-\bar x)}^2}}}}{n}}$.
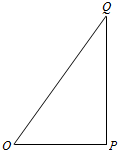 如图,O,P,Q三地有直道相通,OP=3千米,PQ=4千米,OQ=5千米,现甲、乙两警员同时从O地出发匀速前往Q地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是OQ,速度为5千米/小时,乙的路线是OPQ,速度为8千米/小时,乙到达Q地后在原地等待.设t=t1时乙到达P地,t=t2时乙到达Q地.
如图,O,P,Q三地有直道相通,OP=3千米,PQ=4千米,OQ=5千米,现甲、乙两警员同时从O地出发匀速前往Q地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是OQ,速度为5千米/小时,乙的路线是OPQ,速度为8千米/小时,乙到达Q地后在原地等待.设t=t1时乙到达P地,t=t2时乙到达Q地.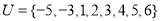 ,集合
,集合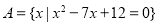 ,集合
,集合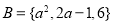 .若
.若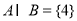 ,且
,且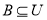 ,则
,则 等于( )
等于( )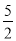 B.
B.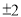
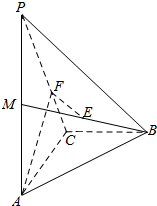 如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.
如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.