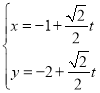题目内容
【题目】椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆的方程;
(2)M,N是椭圆上关于x轴对称的两点,P是椭圆上不同于M,N的一点,直线PM,PN交x轴于D(xD,0)E(xE,0),证明:xDxE为定值.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)由已知条件圆与直线![]() 相切,求出
相切,求出![]() ,再由离心率结合
,再由离心率结合![]() 关系,即可求解;
关系,即可求解;
(2)设M(x0,y0),N(x0,﹣y0),P(xP,yP),求出直线PM,PN方程,进而求出![]() 坐标,结合点
坐标,结合点![]() 在椭圆上,即可证明结论.
在椭圆上,即可证明结论.
(1)由题意e![]() ,b
,b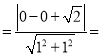 1,
1,
所以a![]() ,
,
因此求椭圆的方程![]() ;
;
(2)证明:设M(x0,y0),N(x0,﹣y0),P(xP,yP),
则直线PM:y﹣y0![]() (x﹣x0),
(x﹣x0),
令y=0,得xD![]() x0,
x0,
同理直线PN:y+y0![]() (x﹣x0),
(x﹣x0),
得xE![]() x0,
x0,
所以xDxE=(![]() x0)(
x0)(![]() x0)
x0)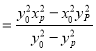 ,①
,①
又![]() ,
,![]() ,
,
则x02=2(1﹣y02),xP2=2(1﹣yP2),代入① 整理得xDxE=2
所以xDxE为定值2.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案【题目】基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验,某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月的市场占有率![]() 进行了统计,结果如表:
进行了统计,结果如表:
月份 |
|
|
|
|
|
|
月份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 11 | 13 | 16 | 15 | 20 | 21 |
![]() 请用相关系数说明能否用线性回归模型拟合y与月份代码x之间的关系,如果能,请计算出y关于x的线性回归方程,并预测该公司2018年12月的市场占有率
请用相关系数说明能否用线性回归模型拟合y与月份代码x之间的关系,如果能,请计算出y关于x的线性回归方程,并预测该公司2018年12月的市场占有率![]() 如果不能,请说明理由.
如果不能,请说明理由.
![]() 根据调研数据,公司决定再采购一批单车扩大市场,现有采购成本分别为1000元
根据调研数据,公司决定再采购一批单车扩大市场,现有采购成本分别为1000元![]() 辆和800元
辆和800元![]() 辆的A,B两款车型,报废年限各不相同
辆的A,B两款车型,报废年限各不相同![]() 考虑公司的经济效益,该公司决定对两款单车进行科学模拟测试,得到两款单车使用寿命频数表如表:
考虑公司的经济效益,该公司决定对两款单车进行科学模拟测试,得到两款单车使用寿命频数表如表:
报废年限 车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 10 | 30 | 40 | 20 | 100 |
B | 15 | 40 | 35 | 10 | 100 |
经测算,平均每辆单车每年可以为公司带来收入500元![]() 不考虑除采购成本以外的其他成本,假设每辆单车的使用寿命都是整数年,用频率估计每辆车使用寿命的概率,分别以这100辆单车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择釆购哪款车型?
不考虑除采购成本以外的其他成本,假设每辆单车的使用寿命都是整数年,用频率估计每辆车使用寿命的概率,分别以这100辆单车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择釆购哪款车型?
参考数据:![]() ,
,![]() ,
,![]()
参考公式:相关系数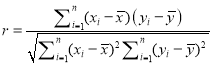
回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为: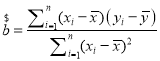 ,
,![]() .
.