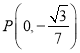题目内容
【题目】甲、乙两个排球队在采用![]() 局
局![]() 胜制排球决赛中相遇,已知每局比赛中甲获胜的概率是
胜制排球决赛中相遇,已知每局比赛中甲获胜的概率是![]() .
.
(1)求比赛进行了![]() 局就结束的概率;
局就结束的概率;
(2)若第![]() 局甲胜,两队又继续进行了
局甲胜,两队又继续进行了![]() 局结束比赛,求
局结束比赛,求![]() 的分布列和数学期望
的分布列和数学期望
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() .
.
【解析】
(1)根据题意可知,比赛进行了![]() 局就结束包含两种情况:一是
局就结束包含两种情况:一是![]() 局全都是甲赢,二是
局全都是甲赢,二是![]() 局全都是乙赢,然后利用独立事件的概率乘法公式可计算出所求事件的概率;
局全都是乙赢,然后利用独立事件的概率乘法公式可计算出所求事件的概率;
(2)由题意可知,随机变量![]() 的可能取值有
的可能取值有![]() 、
、![]() 、
、![]() ,利用独立事件的概率乘法公式计算出
,利用独立事件的概率乘法公式计算出![]() 在不同取值下的概率,可得出随机变量
在不同取值下的概率,可得出随机变量![]() 的概率分布列,进而可计算出随机变量
的概率分布列,进而可计算出随机变量![]() 的数学期望.
的数学期望.
(1)由题意知,每局比赛中乙胜的概率是![]() ,比赛进行了
,比赛进行了![]() 局就结束包括甲
局就结束包括甲![]() 胜和乙
胜和乙![]() 胜两种情况,所以所求概率为
胜两种情况,所以所求概率为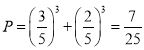 ;
;
(2)由题意知![]() 的可能取值为
的可能取值为![]() 、
、![]() 、
、![]() ,
,
![]() ,
,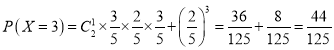 ,
,
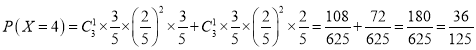 .
.
所以,随机变量![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
所以![]() .
.

练习册系列答案
相关题目
【题目】某公司组织开展“学习强国”的学习活动,活动第一周甲、乙两个部门员工的学习情况统计如下:
学习活跃的员工人数 | 学习不活跃的员工人数 | |
甲 | 18 | 12 |
乙 | 32 | 8 |
(1)从甲、乙两个部门所有员工中随机抽取1人,求该员工学习活跃的概率;
(2)根据表中数据判断能否有![]() 的把握认为员工学习是否活跃与部门有关;
的把握认为员工学习是否活跃与部门有关;
(3)活动第二周,公司为检查学习情况,从乙部门随机抽取2人,发现这两人学习都不活跃,能否认为乙部门第二周学习的活跃率比第一周降低了?
参考公式: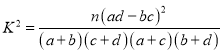 ,其中
,其中![]() .
.
参考数据:![]() ,
,![]() ,
,![]() .
.