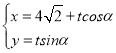��Ŀ����
����Ŀ��2018�����ƹ���ܾ����ں����ʴ����У�����ʱ��Ϊ12��13��12��16�գ������ӵ�����Ŀ���й�����ѡ��4�˲μ�.��֪����һ�߶ӹ�6����Ա�����߶ӹ�4����Ա.
��1����ǡ����3������һ�߶Ӷ�Ա�μӱ����ĸ��ʣ�
��2�����������X��ʾ�μӱ����Ĺ��Ҷ��߶Ӷ�Ա����������X�ķֲ��У�
��3�����ӵ���������ָ�Զ���й��������ű��Ǻͣ��ձ��������������߾���ʤ�ƣ���֪��ÿ�ֱ����У��ָ�Զ��ʤ�ĸ���Ϊ![]() ���ű��Ǻͻ�ʤ�ĸ���Ϊ
���ű��Ǻͻ�ʤ�ĸ���Ϊ![]() ��ǰ���ֱ���˫����ʤһ�֣��Ҹ��ֱ����Ľ������������ָ�Զ������ӵ���ھ��ĸ���.
��ǰ���ֱ���˫����ʤһ�֣��Ҹ��ֱ����Ľ������������ָ�Զ������ӵ���ھ��ĸ���.
���𰸡���1��![]() ����2���ֲ��м���������3��
����2���ֲ��м���������3��![]()
��������
��1������һ�߶ӹ�6����Ա�����߶ӹ�4����Ա��ѡ��4�˲μӱ����������¼�����![]() ��ǡ����3������һ�߶Ӷ�Ա�μӱ��������Ļ����¼�����
��ǡ����3������һ�߶Ӷ�Ա�μӱ��������Ļ����¼�����![]() ���ɴ������ǡ����3������һ�߶Ӷ�Ա�μӱ����ĸ��ʣ� ��2��
���ɴ������ǡ����3������һ�߶Ӷ�Ա�μӱ����ĸ��ʣ� ��2��![]() ��ȡֵΪ0��1��2��3��4���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��У� ��3���ֱ����
��ȡֵΪ0��1��2��3��4���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��У� ��3���ֱ����![]() ��ʤ��
��ʤ��![]() ��ʤ��
��ʤ��![]() ��ʤ�ĸ��ʣ��ɴ����û����¼����ʼӷ���ʽ������ָ�Զ��ùھ��ĸ��ʣ�
��ʤ�ĸ��ʣ��ɴ����û����¼����ʼӷ���ʽ������ָ�Զ��ùھ��ĸ��ʣ�
(1)����һ�߶ӹ�6����Ա�����߶ӹ�4����Ա.ѡ��4�˲μӱ�����
�����¼�����![]() ��
��
ǡ����3������һ�߶Ӷ�Ա�μӱ��������Ļ����¼�����![]() ��
��
��ǡ����3������һ�߶Ӷ�Ա�μӱ����ĸ���p![]() .
.
(2)![]() ��ȡֵΪ0��1��2��3��4��
��ȡֵΪ0��1��2��3��4��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��X�ķֲ���Ϊ��
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
(3)![]() ��ʤ�ĸ���
��ʤ�ĸ���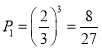 ��
��
![]() ��ʤ�ĸ���
��ʤ�ĸ���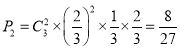 ��
��
![]() ��ʤ�ĸ���
��ʤ�ĸ���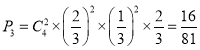 ��
��
�����ָ�Զ��ùھ��ĸ���Ϊ![]() .
.

 �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�