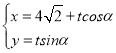题目内容
【题目】已知函数
（
）的图象为曲线
．
（Ⅰ）求曲线上任意一点处的切线的斜率的取值范围；
（Ⅱ）若曲线上存在两点处的切线互相垂直，求其中一条切线与曲线的切点的横坐标的取值范围；
（Ⅲ）试问：是否存在一条直线与曲线C同时切于两个不同点？如果存在，求出符合条件的所有直线方程；若不存在，说明理由．
【答案】(1)
(2)
(3) 不存在一条直线与曲线C同时切于两点
【解析】
试题解：（Ⅰ）
，则
，
即曲线
上任意一点处的切线的斜率的取值范围是；
（Ⅱ）由（1）可知，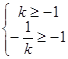
解得
或
，由
或
得：；
（Ⅲ）设存在过点A
的切线曲线C同时切于两点，另一切点为B
，
，
则切线方程是：
，
化简得：
，
而过B的切线方程是
，
由于两切线是同一直线，
则有：
，得
，
又由
，
即
，即
即
，
得
，但当时，由
得
，这与矛盾．
所以不存在一条直线与曲线C同时切于两点.
练习册系列答案
相关题目
【题目】某公司组织开展“学习强国”的学习活动，活动第一周甲、乙两个部门员工的学习情况统计如下：
学习活跃的员工人数 | 学习不活跃的员工人数 | |
甲 | 18 | 12 |
乙 | 32 | 8 |
（1）从甲、乙两个部门所有员工中随机抽取1人，求该员工学习活跃的概率；
（2）根据表中数据判断能否有
的把握认为员工学习是否活跃与部门有关；
（3）活动第二周，公司为检查学习情况，从乙部门随机抽取2人，发现这两人学习都不活跃，能否认为乙部门第二周学习的活跃率比第一周降低了？
参考公式：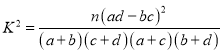
，其中
.
参考数据：
，
，
.
