题目内容
17.对于不重合的两个平面α和β,给定下列条件:①存在直线l,使得l⊥α,且l⊥β;
②存在平面γ,使得α⊥γ且β⊥γ;
③存在平面γ,使得γ∥α且γ∥β;
④α内有不共线的三点到β的距离相等;
其中,可以判定α与β平行的条件有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用平面与平面的判定定理,即可得出结论.
解答 解:①存在直线l,使得l⊥α,且l⊥β,可得α与β平行;
②存在平面γ,使得α⊥γ且β⊥γ,可得α与β平行或相交;
③存在平面γ,使得γ∥α且γ∥β,α与β平行;
④α内有不共线的三点到β的距离相等,可得α与β平行或相交.
故选:B.
点评 本题考查平面与平面的判定定理,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
7.设函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}\\;x<0}\\{g(x)\\;x>0}\end{array}\right.$,若f(x)是奇函数,则g(2)的值是( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
8.如果命题“坐标满足方程F(x,y)=0的点都在曲线C上”是不正确的,那么下列命题正确的是( )
| A. | 坐标满足方程F(x,y)=0的点都不在曲线C上 | |
| B. | 曲线C上的点的坐标不都满足方程F(x,y)=0 | |
| C. | 坐标满足方程F(x,y)=0的点,有些在曲线C上,有些不在曲线C上 | |
| D. | 至少有一个不在曲线C上的点,它的坐标满足F(x,y)=0. |
9.“若随机事件A,B相互独立,则P(A∩B)=P(A)P(B)”的逆否命题是( )
| A. | “若随机事件A,B相互不独立,则P(A∩B)≠P(A)P(B)” | |
| B. | “若随机事件A,B相互独立,则P(A∩B)≠P(A)P(B)” | |
| C. | “若P(A∩B)=P(A)P(B),则随机事件A,B相互不独立” | |
| D. | “若P(A∩B)≠P(A)P(B),则随机事件A,B相互不独立” |
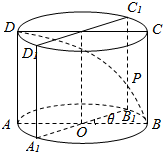 已知圆柱OO1底面半径为1,高为π,ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线Γ如图所示.现将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ≤π)后,边B1C1与曲线Γ相交于点P,设BP的长度为f(θ),则y=f(θ)的图象大致为( )
已知圆柱OO1底面半径为1,高为π,ABCD是圆柱的一个轴截面.动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线Γ如图所示.现将轴截面ABCD绕着轴OO1逆时针旋转θ(0<θ≤π)后,边B1C1与曲线Γ相交于点P,设BP的长度为f(θ),则y=f(θ)的图象大致为( )