题目内容
2．
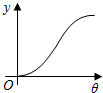已知圆柱OO1底面半径为1，高为π，ABCD是圆柱的一个轴截面．动点M从点B出发沿着圆柱的侧面到达点D，其距离最短时在侧面留下的曲线Γ如图所示．现将轴截面ABCD绕着轴OO1逆时针旋转θ（0＜θ≤π）后，边B1C1与曲线Γ相交于点P，设BP的长度为f（θ），则y=f（θ）的图象大致为（ ）| A． |  | B． |  | C． |  | D． |  |
分析 将圆柱一半展开后底面的半个圆周变成长方形的边BA，曲线Γ就是对角线BD，即可得出结论．
解答 解：（1）将圆柱一半展开后底面的半个圆周变成长方形的边BA，曲线Γ就是对角线BD．
边B1C1与曲线Γ相交于点P，设BP的长度为f（θ），y=f（θ）的图象是一条射线，
故选：A．
点评 本题考查轨迹问题，考查函数的图象，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
13．已知F1，F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两焦点，以点F1为直角顶点作等腰直角三角形MF1F2，若边MF1的中点在双曲线上，则双曲线的离心率是（ ）
| A． | $\frac{{\sqrt{5}+1}}{2}$ | B． | $\sqrt{5}-1$ | C． | $\sqrt{5}+1$ | D． | $\frac{{\sqrt{5}}}{2}$ |
17．对于不重合的两个平面α和β，给定下列条件：
①存在直线l，使得l⊥α，且l⊥β；
②存在平面γ，使得α⊥γ且β⊥γ；
③存在平面γ，使得γ∥α且γ∥β；
④α内有不共线的三点到β的距离相等；
其中，可以判定α与β平行的条件有（ ）
①存在直线l，使得l⊥α，且l⊥β；
②存在平面γ，使得α⊥γ且β⊥γ；
③存在平面γ，使得γ∥α且γ∥β；
④α内有不共线的三点到β的距离相等；
其中，可以判定α与β平行的条件有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
14．已知A（1，-2，11）、B（4，2，3）、C（x，y，15）三点共线，则xy等于（ ）
| A． | 0 | B． | 2 | C． | 4 | D． | 5 |
11．已知一个底面是菱形的直棱柱的侧棱长为5，菱形的对角线的长分别是9和15，则这个棱柱的侧面积是（ ）
| A． | 30$\sqrt{34}$ | B． | 60$\sqrt{34}$ | C． | 30$\sqrt{34}$+135 | D． | 135 |
12．函数f（x）=|lgx2|为（ ）
| A． | 奇函数，在区间（1，+∞）上是减函数 | B． | 奇函数，在区间（1，+∞）上是增函数 | ||
| C． | 偶函数，在区间（0，1）上是增函数 | D． | 偶函数，在区间（0，1）上是减函数． |