题目内容
在直角坐标系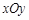 中,点
中,点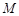 到点
到点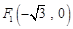 ,
,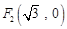 的距离之和是
的距离之和是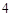 ,点
,点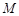 的轨迹
的轨迹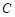 与
与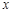 轴的负半轴交于点
轴的负半轴交于点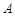 ,不过点
,不过点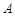 的直线
的直线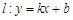 与轨迹
与轨迹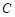 交于不同的两点
交于不同的两点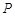 和
和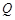 .
.
⑴求轨迹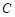 的方程;
的方程;
⑵当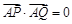 时,证明直线
时,证明直线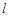 过定点.
过定点.
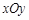 中,点
中,点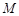 到点
到点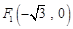 ,
,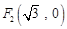 的距离之和是
的距离之和是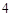 ,点
,点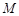 的轨迹
的轨迹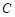 与
与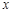 轴的负半轴交于点
轴的负半轴交于点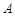 ,不过点
,不过点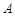 的直线
的直线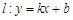 与轨迹
与轨迹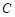 交于不同的两点
交于不同的两点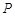 和
和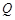 .
.⑴求轨迹
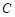 的方程;
的方程;⑵当
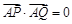 时,证明直线
时,证明直线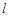 过定点.
过定点.⑴∵点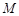 到
到 ,
,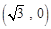 的距离之和是
的距离之和是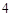 ,∴
,∴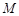 的轨迹
的轨迹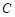 是长轴为
是长轴为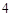 ,焦点在
,焦点在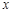 轴上焦距为
轴上焦距为 的椭圆,其方程为
的椭圆,其方程为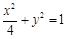 .
.
⑵将 ,代入曲线
,代入曲线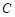 的方程,整理得
的方程,整理得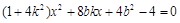 ,因为直线
,因为直线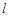 与曲线
与曲线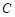 交于不同的两点
交于不同的两点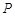 和
和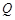 ,所以
,所以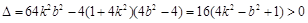 ①
①
设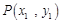 ,
, ,则
,则 ,
, ②
②
且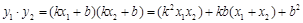 ③
③
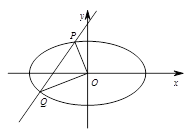
显然,曲线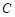 与
与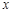 轴的负半轴交于点
轴的负半轴交于点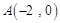 ,所以
,所以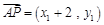 ,
,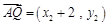 .由
.由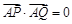 ,得
,得 .
.
将②,③代入上式,整理得 .所以
.所以 ,即
,即 或
或 .经检验,都符合条件①,
.经检验,都符合条件①,
当 时,直线
时,直线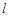 的方程为
的方程为 .显然,此时直线
.显然,此时直线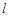 经过定点
经过定点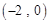 点.即直线
点.即直线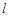 经过点
经过点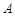 ,与题意不符.
,与题意不符.
当 时,直线
时,直线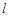 的方程为
的方程为 .显然,此时直线
.显然,此时直线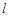 经过定点
经过定点 点,且不过点
点,且不过点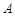 .
.
综上,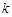 与
与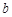 的关系是:
的关系是: ,且直线
,且直线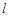 经过定点
经过定点 点.
点.
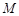 到
到 ,
,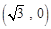 的距离之和是
的距离之和是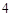 ,∴
,∴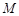 的轨迹
的轨迹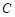 是长轴为
是长轴为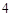 ,焦点在
,焦点在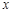 轴上焦距为
轴上焦距为 的椭圆,其方程为
的椭圆,其方程为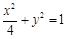 .
. 
⑵将
 ,代入曲线
,代入曲线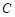 的方程,整理得
的方程,整理得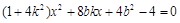 ,因为直线
,因为直线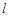 与曲线
与曲线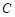 交于不同的两点
交于不同的两点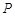 和
和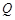 ,所以
,所以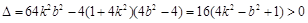 ①
①设
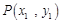 ,
, ,则
,则 ,
, ②
②且
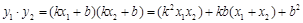 ③
③显然,曲线
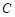 与
与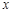 轴的负半轴交于点
轴的负半轴交于点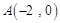 ,所以
,所以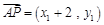 ,
,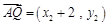 .由
.由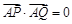 ,得
,得 .
.将②,③代入上式,整理得
 .所以
.所以 ,即
,即 或
或 .经检验,都符合条件①,
.经检验,都符合条件①,当
 时,直线
时,直线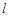 的方程为
的方程为 .显然,此时直线
.显然,此时直线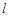 经过定点
经过定点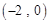 点.即直线
点.即直线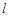 经过点
经过点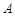 ,与题意不符.
,与题意不符.当
 时,直线
时,直线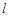 的方程为
的方程为 .显然,此时直线
.显然,此时直线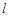 经过定点
经过定点 点,且不过点
点,且不过点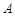 .
.综上,
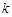 与
与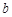 的关系是:
的关系是: ,且直线
,且直线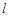 经过定点
经过定点 点.
点.略

练习册系列答案
相关题目
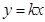 分抛物线
分抛物线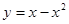 与
与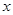 轴所围成图形为面积相等的两个部分,求
轴所围成图形为面积相等的两个部分,求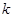 的值.
的值.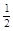 被椭圆x2+4y2=4截得的弦长为 。
被椭圆x2+4y2=4截得的弦长为 。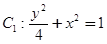 与曲线
与曲线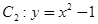 ,设点
,设点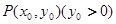 是曲线
是曲线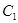 上任意一点,直线
上任意一点,直线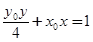 与曲线
与曲线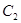 交于
交于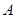 、
、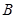 两点.
两点.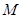 ,求证:点
,求证:点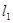 :
: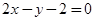 与
与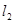 :
: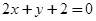 距离的乘积为定值.
距离的乘积为定值.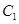 :
: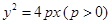 ,焦点为
,焦点为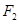 ,其准线与
,其准线与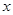 轴交于点
轴交于点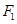 ;椭圆
;椭圆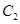 :分别以
:分别以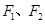 为左、右焦点,其离心率
为左、右焦点,其离心率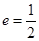 ;且抛物线
;且抛物线 的一个交点记为
的一个交点记为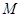 .
.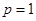 时,求椭圆
时,求椭圆
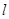 经过椭圆
经过椭圆 与抛物线
与抛物线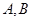 两点,若弦长
两点,若弦长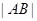 等于
等于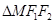 的周长,求直线
的周长,求直线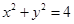 上任取一点
上任取一点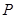 ,过点
,过点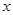 轴的垂线段
轴的垂线段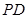 ,
,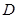 为垂足,当点
为垂足,当点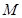 的轨迹为曲线
的轨迹为曲线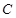
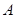
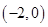 的直线
的直线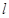 与曲线
与曲线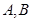 , 点
, 点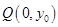 在线段
在线段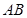 的垂直平分线上,且
的垂直平分线上,且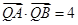 ,求
,求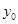 的值
的值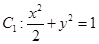 ,抛物线
,抛物线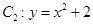 ,点
,点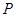 是
是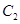 上的动点,过点
上的动点,过点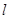 ,交椭圆
,交椭圆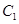 于
于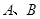 两点,
两点,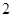 时,求
时,求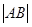 ;
;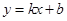 ,当
,当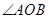 是锐角时,求
是锐角时,求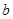 的取值范围.
的取值范围.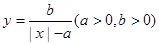 与
与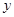 轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 .
轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 .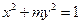 的焦点在
的焦点在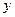 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则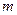 的值为________
的值为________