题目内容
在圆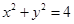 上任取一点
上任取一点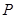 ,过点
,过点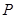 作
作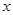 轴的垂线段
轴的垂线段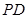 ,
,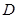 为垂足,当点
为垂足,当点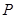 在圆上运动时,线段
在圆上运动时,线段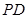 的中点
的中点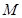 的轨迹为曲线
的轨迹为曲线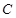
(Ⅰ)求曲线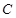 的方程;
的方程;
(Ⅱ)过点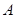
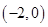 的直线
的直线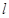 与曲线
与曲线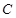 相交于不同的两点
相交于不同的两点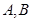 , 点
, 点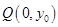 在线段
在线段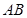 的垂直平分线上,且
的垂直平分线上,且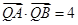 ,求
,求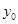 的值
的值
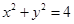 上任取一点
上任取一点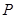 ,过点
,过点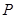 作
作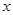 轴的垂线段
轴的垂线段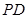 ,
,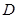 为垂足,当点
为垂足,当点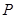 在圆上运动时,线段
在圆上运动时,线段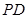 的中点
的中点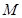 的轨迹为曲线
的轨迹为曲线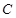
(Ⅰ)求曲线
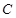 的方程;
的方程;(Ⅱ)过点
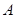
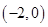 的直线
的直线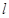 与曲线
与曲线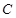 相交于不同的两点
相交于不同的两点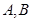 , 点
, 点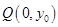 在线段
在线段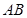 的垂直平分线上,且
的垂直平分线上,且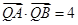 ,求
,求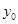 的值
的值设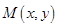 ,则由题意知
,则由题意知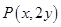 ,又点
,又点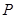 在圆上,将
在圆上,将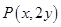 代入圆的方程整理得:
代入圆的方程整理得: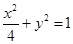 ,即为所求曲线
,即为所求曲线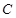 的方程。····························5分
的方程。····························5分
(Ⅱ)设点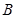
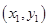 ,由题意直线
,由题意直线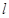 的斜率存在,设直线
的斜率存在,设直线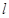 的方程为
的方程为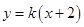 。于是
。于是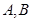 两点的坐标满足方程组
两点的坐标满足方程组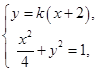 消去
消去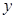 并整理得
并整理得
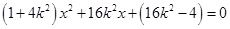 ,
,
因为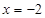 是方程的一个根,则由韦达定理有
是方程的一个根,则由韦达定理有
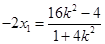 ,所以
,所以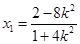 ,从而
,从而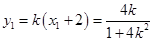 .
.
线段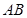 的中点为
的中点为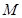 ,则
,则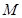 的坐标为
的坐标为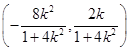 .
.
下面分情况讨论:
(1) 当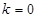 时,点
时,点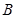 的坐标为
的坐标为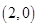 ,线
,线 段
段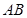 的垂直平分线为
的垂直平分线为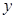 轴.
轴.
于是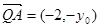 ,
,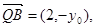 由
由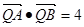 ,得
,得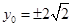 .
.
(2) 当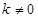 时,线段
时,线段
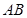 的垂直平分线方程为
的垂直平分线方程为
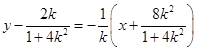 .令
.令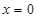 得
得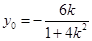
由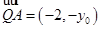 ,
,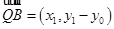 ,
,
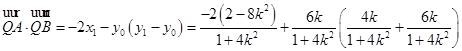
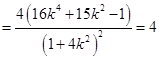 .整理得
.整理得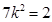 .
.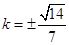 .所以
.所以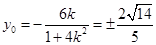 .
.
综上,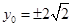 或
或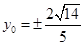
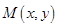 ,则由题意知
,则由题意知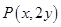 ,又点
,又点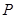 在圆上,将
在圆上,将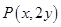 代入圆的方程整理得:
代入圆的方程整理得: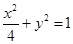 ,即为所求曲线
,即为所求曲线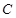 的方程。····························5分
的方程。····························5分(Ⅱ)设点
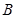
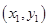 ,由题意直线
,由题意直线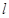 的斜率存在,设直线
的斜率存在,设直线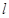 的方程为
的方程为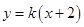 。于是
。于是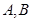 两点的坐标满足方程组
两点的坐标满足方程组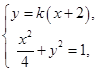 消去
消去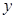 并整理得
并整理得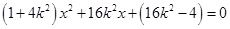 ,
,因为
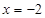 是方程的一个根,则由韦达定理有
是方程的一个根,则由韦达定理有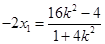 ,所以
,所以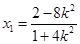 ,从而
,从而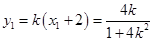 .
.线段
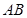 的中点为
的中点为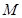 ,则
,则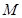 的坐标为
的坐标为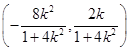 .
.下面分情况讨论:
(1) 当
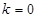 时,点
时,点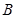 的坐标为
的坐标为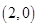 ,线
,线 段
段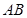 的垂直平分线为
的垂直平分线为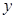 轴.
轴.于是
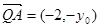 ,
,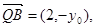 由
由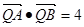 ,得
,得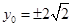 .
.(2) 当
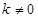 时,线段
时,线段
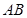 的垂直平分线方程为
的垂直平分线方程为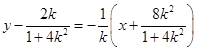 .令
.令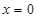 得
得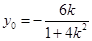
由
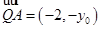 ,
,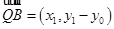 ,
,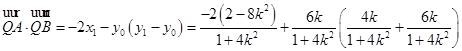
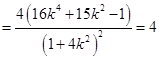 .整理得
.整理得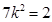 .
.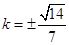 .所以
.所以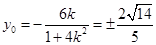 .
. 综上,
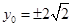 或
或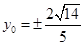
略

练习册系列答案
相关题目
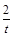 )(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
)(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.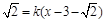 的距离为
的距离为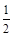 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.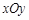 中,点
中,点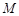 到点
到点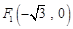 ,
,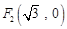 的距离之和是
的距离之和是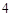 ,点
,点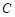 与
与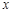 轴的负半轴交于点
轴的负半轴交于点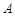 ,不过点
,不过点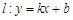 与轨迹
与轨迹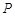 和
和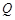 .
.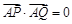 时,证明直线
时,证明直线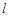 过定点.
过定点.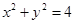 上各点的纵坐标缩短到原来的
上各点的纵坐标缩短到原来的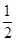 (横坐标不变),所得曲线的方程是( )
(横坐标不变),所得曲线的方程是( )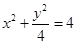
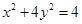
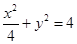
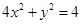
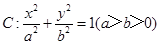 的离心率为
的离心率为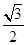 ,过右焦点
,过右焦点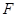 且斜率为
且斜率为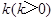 的直线与
的直线与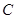 相交于
相交于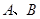 两点.若
两点.若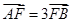 ,则
,则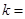
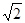 )与曲线x2-y2=1(x>0)相交于A、B两点,则直线l的倾斜角范围是( )
)与曲线x2-y2=1(x>0)相交于A、B两点,则直线l的倾斜角范围是( )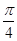 ,
,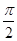 )∪(
)∪(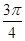 )
)

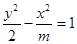 的离心率等于2,则实数
的离心率等于2,则实数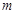 等于( )
等于( )