题目内容
【题目】已知平面内一动点
与两定点
和
连线的斜率之积等于
.
（Ⅰ）求动点
的轨迹
的方程；
（Ⅱ）设直线
： 
（
）与轨迹
交于
、
两点，线段
的垂直平分线交
轴于点
，当
变化时，求
面积的最大值.
【答案】（Ⅰ）
（
）;（Ⅱ）
.
【解析】试题分析：（1）设点的坐标列式，即可求椭圆E的方程；
（2）首先设A（x1，y1），B（x2，y2），将直线y=x+m代入椭圆方程根据韦达定理与判别式求出x1+x2、x1x2和m2的范围，进而求出|AB|，设AB中点
，求出
和
的坐标即可得到
到
的距离
，可得
，可求出三角形面积的最大值.
试题解析：（Ⅰ）设
的坐标为
，
依题意得
，
化简得轨迹
的方程为
（
）.
（Ⅱ）设
， 
，
联立方程组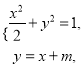
化简得： 
,
有两个不同的交点，
由根与系数的关系得
， 
，
，即
且
.
设
、
中点为
， 
点横坐标
， 
，
，
线段
的垂直平分线方程为
.
点坐标为
.
到
的距离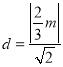
，
由弦长公式得
，
，
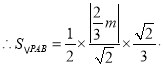
当且仅当
即
时等号成立，
.
点晴:本题主要考查直线与圆锥曲线位置关系. 直线和圆锥曲线的位置关系一方面要体现方程思想，另一方面要结合已知条件，从图形角度求解．联立直线与圆锥曲线的方程得到方程组，化为一元二次方程后由根与系数的关系求解是一个常用的方法. 涉及弦长的问题中，应熟练地利用根与系数关系、设而不求法计算弦长；涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算；涉及过焦点的弦的问题，可考虑用圆锥曲线的定义求解．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
