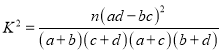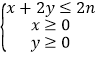题目内容
【题目】某商场一年购进某种货物900吨，每次都购进x吨，运费为每次9万元，一年的总存储费用为9x万元．
（1）要使一年的总运费与总存储费用之和最小，则每次购买多少吨？
（2）要使一年的总运费与总存储费用之和不超过585万元，则每次购买量在什么范围？
【答案】
（1）解：设每次都购买x吨，则需要购买 
次，
∵运费为9万/次，一年的总存储费用为9x万元，
∴一年的总运费与总存储费用之和为9× +9x万元
∵9× +9x≥540，当且仅当9× =9x时取等号
∴x=30吨时，一年的总运费与总存储费用之和最小
（2）解：由题意，9× +9x≤585，得20≤x≤45．
∴每次购买量在大于或等于20吨且小于或等于45吨的范围内
【解析】（1）先设某公司每次都购买x吨，由于一年购买某种货物900吨，得出需要购买的次数，从而求得一年的总运费与总存储费用之和，最后利用基本不等式求得一年的总运费与总存储费用之和最小即可．（2）根据一年的总运费与总存储费用之和不超过585万元，可建立不等式，从而可求次购买量的范围
口算能手系列答案【题目】某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体
名学生中随机抽取了
名学生的体检表，并得到如图的频率分布直方图．
年级名次 是否近视 |
|
|
近视 |
|
|
不近视 |
|
|
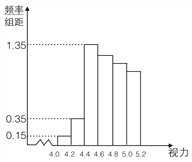
（1）若直方图中后四组的频数成等差数列，试估计全年级视力在
以下的人数；
（2）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在
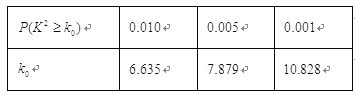
名和
名的学生进行了调查，得到右表中数据，根据表中的数据，能否在犯错的概率不超过
的前提下认为视力与学习成绩有关系?
（3）在（Ⅱ）中调查的
名学生中，按照分层抽样在不近视的学生中抽取了
人，进一步调查他们良好的护眼习惯，并且在这
人中任取
人，记名次在
的学生人数为
，求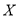
的分布列和数学期望．
|
|
|
|
|
|
|
|
|
|
| 7.879 |
附： 
