题目内容
【题目】已知椭圆![]() 的右焦点为F,直线l与C交于M,N两点.
的右焦点为F,直线l与C交于M,N两点.
(1)若l过点F,点M,N到直线y=2的距离分别为d1,d2,且![]() ,求l的方程;
,求l的方程;
(2)若点M的坐标为(0,1),直线m过点M交C于另一点N′,当直线l与m的斜率之和为2时,证明:直线NN′过定点.
【答案】(1)x﹣y﹣1=0或x﹣2y﹣1=0(2)证明见解析;
【解析】
(1)由若l过椭圆的右焦点F(1,0),设直线l的方程为x=my+1,联立直线与椭圆方程,消去x,得交点M,N的纵坐标关系,因为点M,N到直线y=2的距离分别为d1,d2,则d1+d2=2﹣yM+2﹣yN=4﹣(yM+yN)![]() ,转化为m的方程,求得m即可.
,转化为m的方程,求得m即可.
(2)分类讨论,当直线NN'的斜率不存在和存在两种情况,设出直线方程,联立直线与椭圆的方程,消去一个变量,由韦达定理得出N,N'的坐标的关系式,再由当直线l与m的斜率之和为2,列出方程,求出直线方程,即可得直线NN'过定点(﹣1,﹣1).
(1)易知F(1,0),设直线l的方程为x=my+1,
由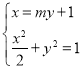 得(m2+2)y2+2my﹣1=0.则yM+yN
得(m2+2)y2+2my﹣1=0.则yM+yN![]() .
.
因为d1+d2=2﹣yM+2﹣yN=4﹣(yM+yN)=4![]() .
.
所以m=1或m=2.
故l的方程为x﹣y﹣1=0或x﹣2y﹣1=0.
(2)证明:当直线NN'的斜率不存在时,设N(x0,y0),则N'(x0,﹣y0).
由kl+km=2,得![]() 2,解得x0=﹣1.
2,解得x0=﹣1.
当直线NN'的斜率存在时,
设直线NN'的方程为y=kx+t(t≠1),N(x1,y1),N'(x2,y2).
由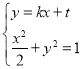 得(1+2k2)x2+4ktx+2t2﹣2=0.
得(1+2k2)x2+4ktx+2t2﹣2=0.
所以x1+x2![]() ,x1x2
,x1x2![]() ;
;
因为kl+km=2.
所以![]() 2k
2k![]() 2k
2k![]() 2k
2k![]() 2.
2.
所以t=k﹣1,所以直线NN'的方程为y=kx+k﹣1,即y+1=k(x+1).
故直线NN'过定点(﹣1,﹣1).
综上,直线NN'过定点(﹣1,﹣1).

【题目】2020年春季受新冠肺炎疫情的影响,利用网络软件办公与学习成为了一种新的生活方式,网上办公软件的开发与使用成为了一个热门话题.为了解“钉钉”软件的使用情况,“钉钉”公司借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
35岁及以下 | 70 | 30 | 100 |
35岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为“钉钉”软件的使用情况与年龄有关?
(2)现从所抽取的35岁以上的网友中利用分层抽样的方法再抽取5人.从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用“钉钉”软件的概率.
参考公式: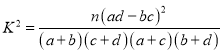 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】已知某快递公司收取快递费的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,在收费
的包裹,在收费![]() 元的基础上,每超过
元的基础上,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了
元.该快递公司承揽了一个工艺品厂家的全部玻璃工艺品包裹的邮寄事宜,该厂家随机统计了![]() 件这种包裹的两个统计数表如下:
件这种包裹的两个统计数表如下:
表![]()
包裹重量 |
|
|
|
|
|
包裹数 |
|
|
|
|
|
损坏件数 |
|
|
|
|
|
表![]()
包裹重量 |
|
|
|
|
|
出厂价(元 |
|
|
|
|
|
卖价(元 |
|
|
|
|
|
![]() 估计该快递公司对每件包裹收取快递费的平均值;
估计该快递公司对每件包裹收取快递费的平均值;
![]() 将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的
将包裹重量落入各组的频率视为概率,该工艺品厂家承担全部运费,每个包裹只有一件产品,如果客户收到有损坏品的包裹,该快递公司每件按其出厂价的![]() 赔偿给厂家.现该厂准备给客户邮寄重量在区间
赔偿给厂家.现该厂准备给客户邮寄重量在区间![]() 和
和![]() 内的工艺品各
内的工艺品各![]() 件,求该厂家这两件工艺品获得利润的分布列和期望.
件,求该厂家这两件工艺品获得利润的分布列和期望.

